Trong không gian với hệ tọa độ Oxyz, cho điểm I(1;1;1) và đường thẳng d: 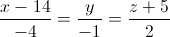 . Viết phương trình mặt cầu (S) tâm I và cắt đường thẳng d tại điểm A và B sao cho AB=16
. Viết phương trình mặt cầu (S) tâm I và cắt đường thẳng d tại điểm A và B sao cho AB=16
DANH SÁCH CÂU HỎI
-
[Trong không gian với hệ tọa độ Oxyz, cho điểm I(1;1;1) và đường thẳng d: - Luyện Tập 365]
-
[Trong không gian với hệ trục Oxyz, cho mặt phẳng (P): 2x + y + 2z + 4 = - Luyện Tập 365]
-
[Trong không gian với hệ tọa độ Oxyz, cho ba đường thẳng d1: < - Luyện Tập 365]
-
[Trong không gian với hệ tọa độ Oxyz, cho d : - Luyện Tập 365]
-
[Trong không gian với hệ trục tọa độ Oxyz, cho hai mặt phẳng (P):2x + y - - Luyện Tập 365]
-
[Trong không gian với hệ tọa độ Oxyz, cho đường thẳng d và mặt cầu (S) có - Luyện Tập 365]
-
[Trong không gian với hệ tọa độ Oxyz, cho ba mặt phẳng (P): x+3y-z+4=0, ( - Luyện Tập 365]
-
[Trong không gian với hệ trục tọa độ Oxyz, cho mặt phẳng (P): x+y-2z+4=0 - Luyện Tập 365]
-
[Trong không gian với hệ tọa độ Oxyz, cho (P):x-y+z-6=0 và hai đường thẳn - Luyện Tập 365]
-
[Trong không gian với hệ tọa độ Oxyz, cho ba mặt phẳng (P): 2x-y+2z-1=0, - Luyện Tập 365]
-
[Trong không gian với hệ tọa độ Oxyz, cho hình thoi ABCD có hai đỉnh A(3; - Luyện Tập 365]
-
[Trong không gian với hệ trục tọa độ Oxyz, cho điểm A(-2;1;0), đường thẳn - Luyện Tập 365]
-
[Trong không gian với hệ tọa độ Oxyz, cho hai đường thẳng d1 - Luyện Tập 365]
-
[Trong không gian với hệ trục tọa độ Oxyz, viết phương trình đường thẳng& - Luyện Tập 365]
-
[Trong không gian với hệ trục tọa độ Oxyz, cho mặt phẳng (P) và đường thẳ - Luyện Tập 365]

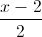 =
= 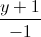 =
= 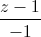 và đường thẳng ∆ là giao tuyến của hai mặt phẳng x = 1, y + z - 4 = 0. Viết phương trình mặt cầu có tâm thuộc d, đồng thời tiếp xúc với ∆ và (P) biết rằng tâm của mặt cầu có tọa độ nguyên.
và đường thẳng ∆ là giao tuyến của hai mặt phẳng x = 1, y + z - 4 = 0. Viết phương trình mặt cầu có tâm thuộc d, đồng thời tiếp xúc với ∆ và (P) biết rằng tâm của mặt cầu có tọa độ nguyên.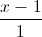 =
= 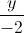 =
= 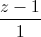 ; d2:
; d2: 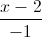 =
= 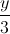 =
= 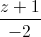 ; d3:
; d3: 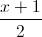 =
= 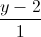 =
= 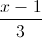 =
= 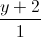 =
= 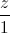 . Và hai mặt phẳng (P): x+y-z+2=0, (Q): x+1=0. Viết phương trình đường thẳng ∆ đi qua M(0;1;1), vuông góc với đường thẳng d đồng thời cắt giao tuyến của hai mặt phẳng (P) và (Q).
. Và hai mặt phẳng (P): x+y-z+2=0, (Q): x+1=0. Viết phương trình đường thẳng ∆ đi qua M(0;1;1), vuông góc với đường thẳng d đồng thời cắt giao tuyến của hai mặt phẳng (P) và (Q).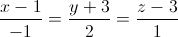 . Viết phương trình mặt cầu (S) có tâm thuộc đường thẳng d, tiếp xúc với (P) và cắt (Q) theo một đường tròn có bán kính r=1
. Viết phương trình mặt cầu (S) có tâm thuộc đường thẳng d, tiếp xúc với (P) và cắt (Q) theo một đường tròn có bán kính r=1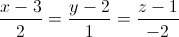 (S): x2+y2+z2-2x+2y-4z -19=0 Tìm điểm M thuộc đường thẳng d sao cho mặt phẳng qua M và vuông góc với đường thẳng d cắt mặt cầu (S) theo một đường tròn có chu vi bằng 8π.
(S): x2+y2+z2-2x+2y-4z -19=0 Tìm điểm M thuộc đường thẳng d sao cho mặt phẳng qua M và vuông góc với đường thẳng d cắt mặt cầu (S) theo một đường tròn có chu vi bằng 8π.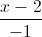 =
=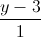 =
=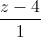 ; d2:
; d2: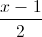 =
=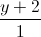 =
=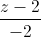 Viết phương trình đường thẳng d biết d//(P) đồng thời d cắt hai đường thẳng d1,d2 lần lượt tại hai điểm A và B sao cho AB=3√6
Viết phương trình đường thẳng d biết d//(P) đồng thời d cắt hai đường thẳng d1,d2 lần lượt tại hai điểm A và B sao cho AB=3√6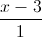 =
=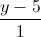 =
=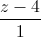 .
.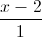 =
= 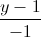 =
= 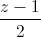 , và mặt phẳng (P): 3x + 2y - 3z - 2 = 0. Gọi B là điểm đối xứng của A qua d. Tìm tọa độ điểm C trong mặt phẳng (P) sao cho đoạn thẳng BC có độ dài nhỏ nhất.
, và mặt phẳng (P): 3x + 2y - 3z - 2 = 0. Gọi B là điểm đối xứng của A qua d. Tìm tọa độ điểm C trong mặt phẳng (P) sao cho đoạn thẳng BC có độ dài nhỏ nhất. 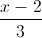 =
= 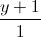 =
= 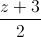 , d2:
, d2: 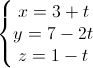 . Viết phương trình đường thẳng ∆ cắt d1và d2 đồng thời đi qua điểm M(3;10;1).
. Viết phương trình đường thẳng ∆ cắt d1và d2 đồng thời đi qua điểm M(3;10;1).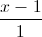 =
=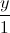 =
=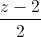 , d':
, d':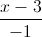 =
=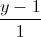 =
=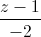 và tạo với đường thẳng d một góc
và tạo với đường thẳng d một góc 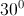 .
.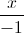 =
=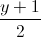 =
=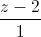 Viết phương trình mặt cầu (S) có tâm thuộc đường thẳng (d), cách mặt phẳng (P) một khoảng bằng 3 và cắt mặt phẳng (P) một khoảng bằng 3 và cắt mặt phẳng (P) theo giao tuyến là đường tròn có bán kính bằng 4.
Viết phương trình mặt cầu (S) có tâm thuộc đường thẳng (d), cách mặt phẳng (P) một khoảng bằng 3 và cắt mặt phẳng (P) một khoảng bằng 3 và cắt mặt phẳng (P) theo giao tuyến là đường tròn có bán kính bằng 4.