Trong mặt phẳng tọa độ Oxy cho đường tròn (C): x2+y2-4x+2y-15=0. Gọi I là tâm đường tròn (C). Đường thẳng ∆ đi qua M(1;-3) cắt (C) tại hai điểm phân biệt A,B. Viết phương trình đường thẳng ∆ biết tam giác IAB có diện tích bằng 8 và cạnh AB là cạnh lớn nhất.

Câu hỏi
Nhận biếtTrong mặt phẳng tọa độ Oxy cho đường tròn (C): x2+y2-4x+2y-15=0. Gọi I là tâm đường tròn (C). Đường thẳng ∆ đi qua M(1;-3) cắt (C) tại hai điểm phân biệt A,B. Viết phương trình đường thẳng ∆ biết tam giác IAB có diện tích bằng 8 và cạnh AB là cạnh lớn nhất.
Đáp án đúng: A
Lời giải của Luyện Tập 365
Đường tròn (C) có tâm I(2;-1), bán kính R=2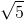 . Gọi H là trung điểm của AB. Đặt AH=x (0<x<2
. Gọi H là trung điểm của AB. Đặt AH=x (0<x<2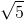 ). Khi đó ta có:
). Khi đó ta có:
 IH.AB=8 <=> x
IH.AB=8 <=> x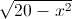 =8 <=>
=8 <=> 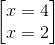 (loại x=2 vì AH<IA)
(loại x=2 vì AH<IA)
Nên AH=4 => IH=2
Phương trình đường thẳng qua M: a(x-1)+b(y+3)=0 (a2+b2 # 0)
<=> ax+by+3b-a=0
Ta có: d(I,AB)=IH=2 <=>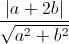 =2 <=> a(3a-4b)=0 <=>
=2 <=> a(3a-4b)=0 <=>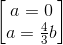
+ Với a=0 ta có phương trình ∆: y+3=0
+ Với a= b. Chọn b=3 ta có a=4. Suy ra phương trình ∆: 4x+3y+5=0
b. Chọn b=3 ta có a=4. Suy ra phương trình ∆: 4x+3y+5=0
Vậy có 2 phương trình ∆ thỏa mãn là y+3=0 và 4x+3y+5=0
Đường tròn (C) có tâm I(2;-1), bán kính R=2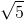 . Gọi H là trung điểm của AB. Đặt AH=x (0<x<2
. Gọi H là trung điểm của AB. Đặt AH=x (0<x<2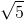 ). Khi đó ta có:
). Khi đó ta có:
 IH.AB=8 <=> x
IH.AB=8 <=> x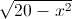 =8 <=>
=8 <=> 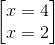 (loại x=2 vì AH<IA)
(loại x=2 vì AH<IA)
Nên AH=4 => IH=2
Phương trình đường thẳng qua M: a(x-1)+b(y+3)=0 (a2+b2 # 0)
<=> ax+by+3b-a=0
Ta có: d(I,AB)=IH=2 <=>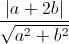 =2 <=> a(3a-4b)=0 <=>
=2 <=> a(3a-4b)=0 <=>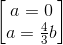
+ Với a=0 ta có phương trình ∆: y+3=0
+ Với a= b. Chọn b=3 ta có a=4. Suy ra phương trình ∆: 4x+3y+5=0
b. Chọn b=3 ta có a=4. Suy ra phương trình ∆: 4x+3y+5=0
Vậy có 2 phương trình ∆ thỏa mãn là y+3=0 và 4x+3y+5=0
Câu hỏi liên quan
-

Trong không gian với hệ trục tọa độ Oxyz, viết phương trình đường thẳng ∆ nằm trong mặt phẳng (P): x+y-z+1=0, cắt các đường thẳng d:
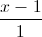 =
=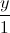 =
=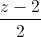 , d':
, d':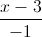 =
=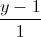 =
=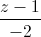 và tạo với đường thẳng d một góc
và tạo với đường thẳng d một góc 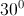 .
. -

Tìm số phức z thỏa mãn
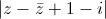 = √5 và (2 - z)(i +
= √5 và (2 - z)(i + 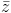 ) là số ảo.
) là số ảo. -

Cho các số thực x,y thỏa mãn x
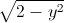 + y
+ y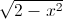 = 2 Tìm giá trị lớn nhất của biểu thức P=
= 2 Tìm giá trị lớn nhất của biểu thức P=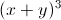 -12(x-1).(y-1)+√xy.
-12(x-1).(y-1)+√xy. -

Giải phương trình
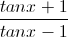 =
=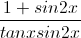
-

Cho hàm số y =
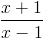 . a) Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số đã cho (HS tự làm). b) Tìm điểm M trên đồ thị (C) sao cho tổng khoảng cách từ M đến các đường thẳng ∆1: 2x + y - 4 = 0 và ∆2: x + 2y - 2 = 0 là nhỏ nhất.
. a) Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số đã cho (HS tự làm). b) Tìm điểm M trên đồ thị (C) sao cho tổng khoảng cách từ M đến các đường thẳng ∆1: 2x + y - 4 = 0 và ∆2: x + 2y - 2 = 0 là nhỏ nhất. -

Tính tích phân I =
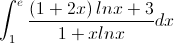
-

Cho các số thực x, y, z không âm thỏa mãn điều kiện x3 + y3 + z3= 2 + 3xyz. Tìm giá trị nhỏ nhất của biểu thức P = x2 + 2y2 + 3z2.
-

Trong không gian với hệ tọa độ Oxyz, cho hai mặt phẳng (α): 2x - y + z - 2 = 0, (β): x + 2y +2z - 4 = 0. Viết phương trình đường thẳng d nằm trong (α), song song với (β) và cách (β) một khoảng bằng 1.
-

Tìm hệ số của x8 trong khai triển Niutơn của
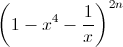 , biết rằng n thỏa mãn
, biết rằng n thỏa mãn 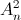 .
.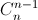 = 180. (
= 180. (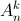 ,
, 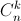 lần lượt là số chỉnh hợp, số tổ hợp chập k của n phần tử).
lần lượt là số chỉnh hợp, số tổ hợp chập k của n phần tử). -

Giải hệ phương trình
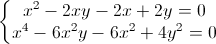 (x, y
(x, y R)
R)
