Cho các số thực x, y thỏa mãn (x – 4)2 + (y – 4)2 + 2xy ≤ 32. Tìm giá trị nhỏ nhất của biểu thức A = x3 + y3 + 3(xy – 1)(x + y – 2).

Câu hỏi
Nhận biếtCho các số thực x, y thỏa mãn (x – 4)2 + (y – 4)2 + 2xy ≤ 32. Tìm giá trị nhỏ nhất của biểu thức A = x3 + y3 + 3(xy – 1)(x + y – 2).
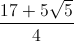 .
. 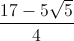 .
. 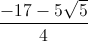 .
. 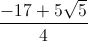 .
. Đáp án đúng: B
Lời giải của Luyện Tập 365
Ta có (x – 4)2 + (y – 4)2 + 2xy ≤ 32 ⇔ (x + y)2 – 8(x + y) ≤ 0 ⇔ 0 ≤ x + y ≤ 8.
A = (x + y)3 – 3(x + y) – 6xy + 6 ≥ (x + y)3 –  (x + y)2 – 3(x + y) + 6.
(x + y)2 – 3(x + y) + 6.
Xét hàm số: f(t) = t3 –  t2 – 3t + 6 trên đoạn [0; 8].
t2 – 3t + 6 trên đoạn [0; 8].
Ta có f’(t) = 3t2 – 3t – 3, f’(t) = 0 ⇔ t = 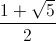 hoặc t =
hoặc t = 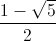 (loại).
(loại).
Ta có f(0) = 6, f(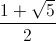 ) =
) = 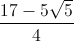 , f(8) = 398. Suy ra A ≥
, f(8) = 398. Suy ra A ≥ 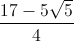 .
.
Khi x = y = 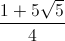 thì dấu bằng xảy ra. Vậy giá trị nhỏ nhất của A là
thì dấu bằng xảy ra. Vậy giá trị nhỏ nhất của A là 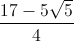 .
.
Ta có (x – 4)2 + (y – 4)2 + 2xy ≤ 32 ⇔ (x + y)2 – 8(x + y) ≤ 0 ⇔ 0 ≤ x + y ≤ 8.
A = (x + y)3 – 3(x + y) – 6xy + 6 ≥ (x + y)3 –  (x + y)2 – 3(x + y) + 6.
(x + y)2 – 3(x + y) + 6.
Xét hàm số: f(t) = t3 –  t2 – 3t + 6 trên đoạn [0; 8].
t2 – 3t + 6 trên đoạn [0; 8].
Ta có f’(t) = 3t2 – 3t – 3, f’(t) = 0 ⇔ t = 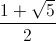 hoặc t =
hoặc t = 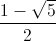 (loại).
(loại).
Ta có f(0) = 6, f(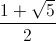 ) =
) = 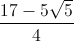 , f(8) = 398. Suy ra A ≥
, f(8) = 398. Suy ra A ≥ 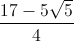 .
.
Khi x = y = 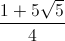 thì dấu bằng xảy ra. Vậy giá trị nhỏ nhất của A là
thì dấu bằng xảy ra. Vậy giá trị nhỏ nhất của A là 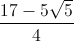 .
.
Câu hỏi liên quan
-

Giải hệ phương trình
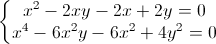 (x, y
(x, y R)
R) -

Giải phương trình sin2x.(tan x - 1) = 3 sin x.(cos x + sin x) - 3.
-

Trong mặt phẳng với hệ trục Oxy, cho hai đường thẳng ∆1: 3x+y+5=0, ∆2: x-2y-3=0 và đường tròn (C):
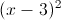 +
+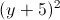 =25. Tìm điểm M thuộc (C), điểm N thuộc đường thẳng ∆1, sao cho M và N đối xứng qua ∆2.
=25. Tìm điểm M thuộc (C), điểm N thuộc đường thẳng ∆1, sao cho M và N đối xứng qua ∆2. -

Trong mặt phẳng với hệ trục Oxy, cho điểm M(4; -3) và đường tròn (C): x2 + y2 - 4x - 2y +1 = 0 với tâm là I. Lập phương trình tổng quát của đường thẳng d đi qua M và cắt đường tròn (C) tại hai điểm phân biệt P, Q sao cho tam giác IPQ vuông.
-

Trong không gian với hệ tọa độ Oxyz, cho hai đường thẳng d1:
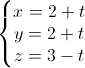 , d2:
, d2: 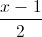 =
= 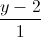 =
= 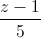 . Viết phương trình mặt phẳng song song và cách đều hai đường thẳng d1 và d2.
. Viết phương trình mặt phẳng song song và cách đều hai đường thẳng d1 và d2. -

Cho hàm số y =x3-6x2+3mx+2, với m là tham số thực. a) Khảo sát sự biến thiên và vẽ đồ thị của hàm số đã cho khi m=3 (HS tự làm). b) Tìm m sao cho đồ thị của hàm số đã cho có các điểm cực trị A,B thỏa mãn AB=4√65.
-

Tìm hệ số của x8 trong khai triển Niutơn của
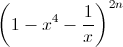 , biết rằng n thỏa mãn
, biết rằng n thỏa mãn 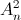 .
.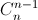 = 180. (
= 180. (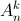 ,
, 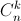 lần lượt là số chỉnh hợp, số tổ hợp chập k của n phần tử).
lần lượt là số chỉnh hợp, số tổ hợp chập k của n phần tử). -

Tìm số phức z thỏa mãn
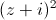 +
+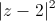 =2
=2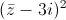 .
. -

Cho hàm số y =
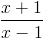 . a) Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số đã cho (HS tự làm). b) Tìm điểm M trên đồ thị (C) sao cho tổng khoảng cách từ M đến các đường thẳng ∆1: 2x + y - 4 = 0 và ∆2: x + 2y - 2 = 0 là nhỏ nhất.
. a) Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số đã cho (HS tự làm). b) Tìm điểm M trên đồ thị (C) sao cho tổng khoảng cách từ M đến các đường thẳng ∆1: 2x + y - 4 = 0 và ∆2: x + 2y - 2 = 0 là nhỏ nhất. -

Một hộp đựng 5 viên bi đỏ, 6 viên xanh và 7 viên bi vàng. Chọn ra 5 viên bi rừ hộp đó. Hỏi có bao nhiêu cách chọn mà 5 viên bi được chọn không có đủ cả 3 màu?
