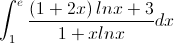Giải hệ phương trình: 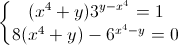

Câu hỏi
Nhận biếtGiải hệ phương trình: 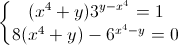
![\left\{\begin{matrix}x=\sqrt[4]{5}\\y=-12\end{matrix}\right.](https://luyentap365.com/wp-content/picture/learning/exam/2013/1121/5348_570800_1.gif)
![\left\{\begin{matrix}x=\pm \sqrt[4]{5}\\y=-12\end{matrix}\right.](https://luyentap365.com/wp-content/picture/learning/exam/2013/1021/5348_b_0.gif)
![\left\{\begin{matrix}x=\sqrt[4]{5}\\y=12\end{matrix}\right.](https://luyentap365.com/wp-content/picture/learning/exam/2013/1121/5348_135572_1.gif)
![\left\{\begin{matrix}x=\pm \sqrt[4]{5}\\y=12\end{matrix}\right.](https://luyentap365.com/wp-content/picture/learning/exam/2013/1021/5348_d_0.gif)
Đáp án đúng: D
Lời giải của Luyện Tập 365
Đặt 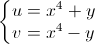 => ta có hệ phương trình
=> ta có hệ phương trình 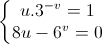
⇔ 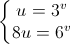
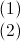
Thay (1) vào (2) : 8.3v = 6v ⇔ 8 = 2v ⇔ v = 3 => u = 27
Ta có 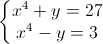 =>
=> ![\left\{\begin{matrix}x=\pm \sqrt[4]{5}\\y=12\end{matrix}\right.](https://luyentap365.com/wp-content/picture/learning/exam/2013/1020/vip_5348_des_0.gif)
Vậy hệ phương trình có hai nghiệm ![\left\{\begin{matrix}x=\pm \sqrt[4]{5}\\y=12\end{matrix}\right.](https://luyentap365.com/wp-content/picture/learning/exam/2013/1020/vip_5348_des_1.gif)
Đặt 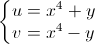 => ta có hệ phương trình
=> ta có hệ phương trình 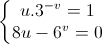
⇔ 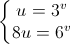
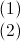
Thay (1) vào (2) : 8.3v = 6v ⇔ 8 = 2v ⇔ v = 3 => u = 27
Ta có 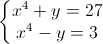 =>
=> ![\left\{\begin{matrix}x=\pm \sqrt[4]{5}\\y=12\end{matrix}\right.](https://luyentap365.com/wp-content/picture/learning/exam/2013/1020/vip_5348_des_0.gif)
Vậy hệ phương trình có hai nghiệm ![\left\{\begin{matrix}x=\pm \sqrt[4]{5}\\y=12\end{matrix}\right.](https://luyentap365.com/wp-content/picture/learning/exam/2013/1020/vip_5348_des_1.gif)
Câu hỏi liên quan
-

Giải phương trình (1-
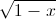 ).
).![\sqrt[3]{2-x}](https://luyentap365.com/wp-content/picture/learning/exam/2013/1031/75_220_2.gif) = x.
= x. -

Cho hàm số y =
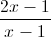 a) Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số. b) Tìm m để đường thẳng d : y = 3x+m cắt đồ thị (C) tại hai điểm A, B sao cho độ dài AB nhỏ nhất.
a) Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số. b) Tìm m để đường thẳng d : y = 3x+m cắt đồ thị (C) tại hai điểm A, B sao cho độ dài AB nhỏ nhất. -

Tìm hệ số của x8 trong khai triển Niutơn của
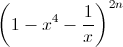 , biết rằng n thỏa mãn
, biết rằng n thỏa mãn 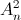 .
.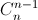 = 180. (
= 180. (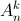 ,
, 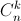 lần lượt là số chỉnh hợp, số tổ hợp chập k của n phần tử).
lần lượt là số chỉnh hợp, số tổ hợp chập k của n phần tử). -

Giải phương trình:
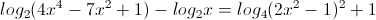
-

Giải hệ phương trình
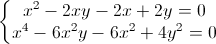 (x, y
(x, y R)
R) -

Cho các số thực x, y, z không âm thỏa mãn điều kiện x3 + y3 + z3= 2 + 3xyz. Tìm giá trị nhỏ nhất của biểu thức P = x2 + 2y2 + 3z2.
-

Giải phương trình
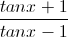 =
=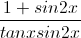
-

Tìm số phức z thỏa mãn
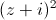 +
+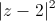 =2
=2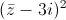 .
. -

Giải phương trình sin2x.(tan x - 1) = 3 sin x.(cos x + sin x) - 3.
-

Tính tích phân I =