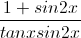Cho hình chóp S.ABCD có đáy ABCD là hình thoi, hai đường chéo AC = 2√3a , BD = 2a và cắt nhau tại O, hai mặt phẳng (SAC) và (SBD) cùng vuông góc với mặt phẳng (ABCD). Biết khoảng cách từ điểm O đến mặt phẳng (SAB) bằng 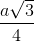 , tính thể tích khối chóp S.ABCD theo a, và góc giữa 2 mặt phẳng (SAB) với (SBD).
, tính thể tích khối chóp S.ABCD theo a, và góc giữa 2 mặt phẳng (SAB) với (SBD).

Câu hỏi
Nhận biếtCho hình chóp S.ABCD có đáy ABCD là hình thoi, hai đường chéo AC = 2√3a , BD = 2a và cắt nhau tại O, hai mặt phẳng (SAC) và (SBD) cùng vuông góc với mặt phẳng (ABCD). Biết khoảng cách từ điểm O đến mặt phẳng (SAB) bằng 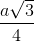 , tính thể tích khối chóp S.ABCD theo a, và góc giữa 2 mặt phẳng (SAB) với (SBD).
, tính thể tích khối chóp S.ABCD theo a, và góc giữa 2 mặt phẳng (SAB) với (SBD).
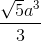 ;
; 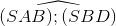 = arccos
= arccos
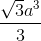 ;
; 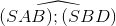 = arccos
= arccos
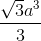 ;
; 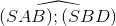 = arccos2
= arccos2 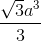 ;
; 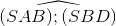 = arccos
= arccos
Đáp án đúng: D
Lời giải của Luyện Tập 365
Từ giả thiết AC = 2a√3; BD = 2a và AC, BD vuông góc với nhau tại trung điểm O của mỗi đường chéo. Ta có ∆ABO vuông tại O và AO = a√3; BO = a. Gọi K là hình chiếu của O trên AB, gọi I là hình chiếu của O trên SK.
Từ giả thiết 2 mặt phẳng (SAC) và (SBD) cùng vuông góc với mặt phẳng (ABCD) nên giao tuyến của chúng là SO ⊥ (ABCD)
Ta chứng minh được khoảng cách O tới (SAB) là đoạn OI
Ta có trong tam giác vuông AOB ta có:
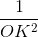 =
= 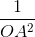 +
+ 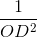 =
= 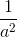 +
+ 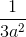 => OK =
=> OK = 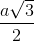
Tam giác SOK vuông tại O, OI là đường cao
=> 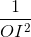 =
= 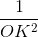 +
+ 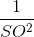 => SO =
=> SO = 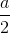 .
.
Diện tích đáy SABCD = 4S∆ABO = 2.OA.OB = 2√3a2
Đường cao của hình chóp SO = 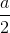
Thể tích khối chóp S.ABCD: VS.ABCD =  SABCD.SO =
SABCD.SO = 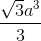
Ta có hình chiếu của tam giác SAB trên mặt phẳng (SBD) là ∆SBO
Gọi α là góc giữa 2 mặt phẳng (SAB) và (SBD) ta có cosα = 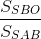
Ta có SSBO =  OB.SO =
OB.SO = 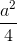 , SK = a => SSAB = a2
, SK = a => SSAB = a2
=> cosα =  => α = arccos
=> α = arccos

Từ giả thiết AC = 2a√3; BD = 2a và AC, BD vuông góc với nhau tại trung điểm O của mỗi đường chéo. Ta có ∆ABO vuông tại O và AO = a√3; BO = a. Gọi K là hình chiếu của O trên AB, gọi I là hình chiếu của O trên SK.
Từ giả thiết 2 mặt phẳng (SAC) và (SBD) cùng vuông góc với mặt phẳng (ABCD) nên giao tuyến của chúng là SO ⊥ (ABCD)
Ta chứng minh được khoảng cách O tới (SAB) là đoạn OI
Ta có trong tam giác vuông AOB ta có:
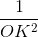 =
= 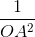 +
+ 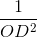 =
= 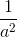 +
+ 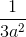 => OK =
=> OK = 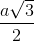
Tam giác SOK vuông tại O, OI là đường cao
=> 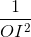 =
= 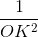 +
+ 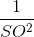 => SO =
=> SO = 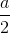 .
.
Diện tích đáy SABCD = 4S∆ABO = 2.OA.OB = 2√3a2
Đường cao của hình chóp SO = 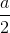
Thể tích khối chóp S.ABCD: VS.ABCD =  SABCD.SO =
SABCD.SO = 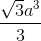
Ta có hình chiếu của tam giác SAB trên mặt phẳng (SBD) là ∆SBO
Gọi α là góc giữa 2 mặt phẳng (SAB) và (SBD) ta có cosα = 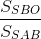
Ta có SSBO =  OB.SO =
OB.SO = 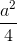 , SK = a => SSAB = a2
, SK = a => SSAB = a2
=> cosα =  => α = arccos
=> α = arccos

Câu hỏi liên quan
-

Tìm số phức z thỏa mãn
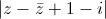 = √5 và (2 - z)(i +
= √5 và (2 - z)(i + 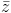 ) là số ảo.
) là số ảo. -

Giải hệ phương trình
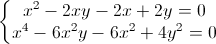 (x, y
(x, y R)
R) -

Cho hàm số y =
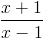 . a) Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số đã cho (HS tự làm). b) Tìm điểm M trên đồ thị (C) sao cho tổng khoảng cách từ M đến các đường thẳng ∆1: 2x + y - 4 = 0 và ∆2: x + 2y - 2 = 0 là nhỏ nhất.
. a) Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số đã cho (HS tự làm). b) Tìm điểm M trên đồ thị (C) sao cho tổng khoảng cách từ M đến các đường thẳng ∆1: 2x + y - 4 = 0 và ∆2: x + 2y - 2 = 0 là nhỏ nhất. -

Cho các số thực x, y thỏa mãn điều kiện x+y=
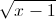 +
+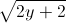 Tìm giá trị lớn nhất, giá trị nhỏ nhất của biểu thức
Tìm giá trị lớn nhất, giá trị nhỏ nhất của biểu thức
P=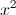 +
+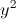 +2(x+1)(y+1)+8
+2(x+1)(y+1)+8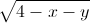
-

Trong mặt phẳng với hệ trục Oxy, cho điểm M(4; -3) và đường tròn (C): x2 + y2 - 4x - 2y +1 = 0 với tâm là I. Lập phương trình tổng quát của đường thẳng d đi qua M và cắt đường tròn (C) tại hai điểm phân biệt P, Q sao cho tam giác IPQ vuông.
-

Tính tích phân I =
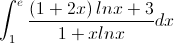
-

Một hộp đựng 5 viên bi đỏ, 6 viên xanh và 7 viên bi vàng. Chọn ra 5 viên bi rừ hộp đó. Hỏi có bao nhiêu cách chọn mà 5 viên bi được chọn không có đủ cả 3 màu?
-

Trong mặt phẳng với hệ trục Oxy, cho tam giác ABC cân, cạnh đáy BC có phương trình x + y + 1 = 0. Phương trình đường cao vẽ từ B là x - 2y - 2 = 0. Điểm M(2; 1) thuộc đường cao vẽ từ C. Viết phương trình các cạnh bên của tam giác ABC.
-

Trong mặt phẳng với hệ trục Oxy, cho hai đường thẳng ∆1: 3x+y+5=0, ∆2: x-2y-3=0 và đường tròn (C):
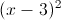 +
+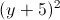 =25. Tìm điểm M thuộc (C), điểm N thuộc đường thẳng ∆1, sao cho M và N đối xứng qua ∆2.
=25. Tìm điểm M thuộc (C), điểm N thuộc đường thẳng ∆1, sao cho M và N đối xứng qua ∆2. -

Giải phương trình
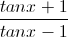 =
=