Trong không gian với hệ tọa độ Oxyz cho tam giác ABC cân tại C có diện tích bằng 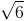 . Biết A(1;-1;2), B(3;1;0). Tìm tọa độ điểm C biết C thuộc mặt phẳng
(P):x-2y-4z+8=0
. Biết A(1;-1;2), B(3;1;0). Tìm tọa độ điểm C biết C thuộc mặt phẳng
(P):x-2y-4z+8=0

Câu hỏi
Nhận biếtTrong không gian với hệ tọa độ Oxyz cho tam giác ABC cân tại C có diện tích bằng 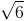 . Biết A(1;-1;2), B(3;1;0). Tìm tọa độ điểm C biết C thuộc mặt phẳng
. Biết A(1;-1;2), B(3;1;0). Tìm tọa độ điểm C biết C thuộc mặt phẳng
(P):x-2y-4z+8=0
Đáp án đúng: D
Lời giải của Luyện Tập 365
AB=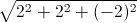 =2
=2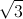
Hạ CH ⊥AB suy ra CH=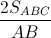 =
=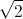
CA=CB=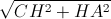 =
=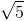
Tọa độ C là nghiệm: 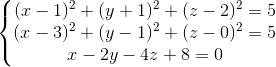
Suy ra C(2;1;2)
AB=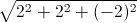 =2
=2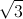
Hạ CH ⊥AB suy ra CH=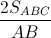 =
=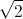
CA=CB=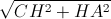 =
=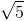
Tọa độ C là nghiệm: 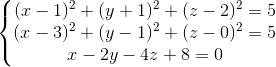
Suy ra C(2;1;2)
Câu hỏi liên quan
-

Cho các số thực x, y thỏa mãn điều kiện x+y=
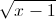 +
+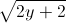 Tìm giá trị lớn nhất, giá trị nhỏ nhất của biểu thức
Tìm giá trị lớn nhất, giá trị nhỏ nhất của biểu thức
P=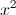 +
+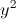 +2(x+1)(y+1)+8
+2(x+1)(y+1)+8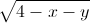
-

Giải phương trình:
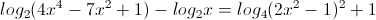
-

Giải phương trình sin2x.(tan x - 1) = 3 sin x.(cos x + sin x) - 3.
-

Tìm số phức z thỏa mãn
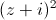 +
+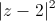 =2
=2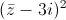 .
. -

Cho hàm số y =
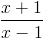 . a) Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số đã cho (HS tự làm). b) Tìm điểm M trên đồ thị (C) sao cho tổng khoảng cách từ M đến các đường thẳng ∆1: 2x + y - 4 = 0 và ∆2: x + 2y - 2 = 0 là nhỏ nhất.
. a) Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số đã cho (HS tự làm). b) Tìm điểm M trên đồ thị (C) sao cho tổng khoảng cách từ M đến các đường thẳng ∆1: 2x + y - 4 = 0 và ∆2: x + 2y - 2 = 0 là nhỏ nhất. -

Trong không gian với hệ trục tọa độ Oxyz, viết phương trình đường thẳng ∆ nằm trong mặt phẳng (P): x+y-z+1=0, cắt các đường thẳng d:
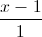 =
=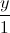 =
=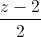 , d':
, d':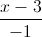 =
=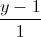 =
=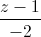 và tạo với đường thẳng d một góc
và tạo với đường thẳng d một góc 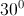 .
. -

Trong mặt phẳng với hệ trục Oxy, cho điểm M(4; -3) và đường tròn (C): x2 + y2 - 4x - 2y +1 = 0 với tâm là I. Lập phương trình tổng quát của đường thẳng d đi qua M và cắt đường tròn (C) tại hai điểm phân biệt P, Q sao cho tam giác IPQ vuông.
-

Giải phương trình
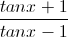 =
=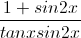
-

Cho các số thực x,y thỏa mãn x
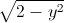 + y
+ y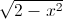 = 2 Tìm giá trị lớn nhất của biểu thức P=
= 2 Tìm giá trị lớn nhất của biểu thức P=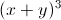 -12(x-1).(y-1)+√xy.
-12(x-1).(y-1)+√xy. -

Tìm số phức z thỏa mãn
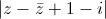 = √5 và (2 - z)(i +
= √5 và (2 - z)(i + 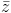 ) là số ảo.
) là số ảo.
