Cho các số thực dương a,b,c thỏa mãn điều kiện |a-b|+|b-c|+|c-a|+3.![\sqrt[3]{abc}](https://luyentap365.com/wp-content/picture/learning/exam/2013/1108/1097_734_1.gif) = 1. Chứng minh rằng: a
= 1. Chứng minh rằng: a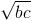 + b
+ b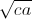 + c
+ c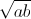 ≤
≤  .
.

Câu hỏi
Nhận biếtCho các số thực dương a,b,c thỏa mãn điều kiện |a-b|+|b-c|+|c-a|+3.![\sqrt[3]{abc}](https://luyentap365.com/wp-content/picture/learning/exam/2013/1108/1097_734_1.gif) = 1. Chứng minh rằng: a
= 1. Chứng minh rằng: a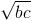 + b
+ b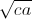 + c
+ c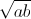 ≤
≤  .
.


Đáp án đúng: B
Lời giải của Luyện Tập 365
Không mất tính tổng quát, giả sử a≥ b≥ c>0. Khi đó, từ giả thiết ta có
1=a-b+b-c+a-c+3![\sqrt[3]{abc}](https://luyentap365.com/wp-content/picture/learning/exam/2013/1108/v1097_241_1.gif) = 2a-2c+3
= 2a-2c+3![\sqrt[3]{abc}](https://luyentap365.com/wp-content/picture/learning/exam/2013/1108/v1097_241_1.gif) ≥ a+b-2c+3c = a+b+c.
≥ a+b-2c+3c = a+b+c.
Khi đó ta có
a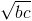 +b
+b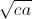 + c
+ c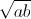 =
= 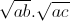 +
+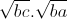 +
+ 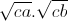
≤ ab+bc+ca ≤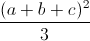 ≤
≤ 
Dấu đẳng thức xảy ra khi và chỉ khi a=b=c= .
.
Nhận xét: Chúng ta có thể giải theo cách khác như sau:
Không mất tính tổng quát, giả sử a≥b≥c>0. Khi đó, từ giả thiết ta có
1=a-b+b-c+a-c+3.![\sqrt[3]{abc}](https://luyentap365.com/wp-content/picture/learning/exam/2013/1108/v1097_241_1.gif) = 2a-2c+
= 2a-2c+![\sqrt[3]{abc}](https://luyentap365.com/wp-content/picture/learning/exam/2013/1108/v1097_241_1.gif) .
.
Ta chứng minh
a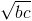 +b
+b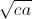 +c
+c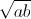 ≤
≤ 
![(2a+\sqrt[3]{abc})^{2}](https://luyentap365.com/wp-content/picture/learning/exam/2013/1108/v1097_110_18.gif) (*)
(*)
Thật vậy bất đẳng thức (*) tương đương với.
3a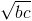 +3b
+3b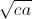 +3c
+3c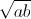 ≤ = 4a2+ 4a.
≤ = 4a2+ 4a.![\sqrt[3]{abc}](https://luyentap365.com/wp-content/picture/learning/exam/2013/1108/v1097_241_1.gif) +
+![\sqrt[3]{abc}^{2}](https://luyentap365.com/wp-content/picture/learning/exam/2013/1114/v1097_147947_23.gif) .
.
Áp dụng bất đẳng thức Côsi và giả thiết a ≥ b ≥ c>0 ta có
= 4a2 +4a.![\sqrt[3]{abc}](https://luyentap365.com/wp-content/picture/learning/exam/2013/1108/v1097_241_1.gif) ≥2
≥2![\sqrt{16a^{3}.\sqrt[3]{abc}}](https://luyentap365.com/wp-content/picture/learning/exam/2013/1108/v1097_677_25.gif) = 8a.
= 8a.![\sqrt[6]{a^{4}bc}](https://luyentap365.com/wp-content/picture/learning/exam/2013/1108/v1097_774_26.gif)
≥ 8a![\sqrt[6]{b^{3}c^{3}}](https://luyentap365.com/wp-content/picture/learning/exam/2013/1108/v1097_234_27.gif) = 8a
= 8a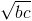 ≥ 3a
≥ 3a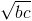 +3b
+3b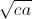 +2c
+2c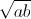
và ![\sqrt[3]{abc}^{2}](https://luyentap365.com/wp-content/picture/learning/exam/2013/1114/v1097_147947_23.gif) =
= ![\sqrt[3]{a^{2}b^{2}c^{2}}](https://luyentap365.com/wp-content/picture/learning/exam/2013/1108/v1097_864_33.gif) ≥ 8a
≥ 8a![\sqrt[3]{a^{\frac{3}{2}}b^{\frac{3}{2}}c^{3}}](https://luyentap365.com/wp-content/picture/learning/exam/2013/1108/v1097_169_34.gif) = c
= c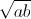
Cộng hai bất đẳng thức trên ta có điều phải chứng minh
Dấu đẳng thức xảy ra khi và chỉ khi a=b=c=
Không mất tính tổng quát, giả sử a≥ b≥ c>0. Khi đó, từ giả thiết ta có
1=a-b+b-c+a-c+3![\sqrt[3]{abc}](https://luyentap365.com/wp-content/picture/learning/exam/2013/1108/v1097_241_1.gif) = 2a-2c+3
= 2a-2c+3![\sqrt[3]{abc}](https://luyentap365.com/wp-content/picture/learning/exam/2013/1108/v1097_241_1.gif) ≥ a+b-2c+3c = a+b+c.
≥ a+b-2c+3c = a+b+c.
Khi đó ta có
a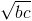 +b
+b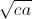 + c
+ c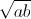 =
= 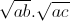 +
+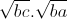 +
+ 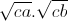
≤ ab+bc+ca ≤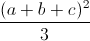 ≤
≤ 
Dấu đẳng thức xảy ra khi và chỉ khi a=b=c= .
.
Nhận xét: Chúng ta có thể giải theo cách khác như sau:
Không mất tính tổng quát, giả sử a≥b≥c>0. Khi đó, từ giả thiết ta có
1=a-b+b-c+a-c+3.![\sqrt[3]{abc}](https://luyentap365.com/wp-content/picture/learning/exam/2013/1108/v1097_241_1.gif) = 2a-2c+
= 2a-2c+![\sqrt[3]{abc}](https://luyentap365.com/wp-content/picture/learning/exam/2013/1108/v1097_241_1.gif) .
.
Ta chứng minh
a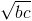 +b
+b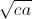 +c
+c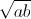 ≤
≤ 
![(2a+\sqrt[3]{abc})^{2}](https://luyentap365.com/wp-content/picture/learning/exam/2013/1108/v1097_110_18.gif) (*)
(*)
Thật vậy bất đẳng thức (*) tương đương với.
3a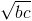 +3b
+3b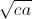 +3c
+3c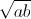 ≤ = 4a2+ 4a.
≤ = 4a2+ 4a.![\sqrt[3]{abc}](https://luyentap365.com/wp-content/picture/learning/exam/2013/1108/v1097_241_1.gif) +
+![\sqrt[3]{abc}^{2}](https://luyentap365.com/wp-content/picture/learning/exam/2013/1114/v1097_147947_23.gif) .
.
Áp dụng bất đẳng thức Côsi và giả thiết a ≥ b ≥ c>0 ta có
= 4a2 +4a.![\sqrt[3]{abc}](https://luyentap365.com/wp-content/picture/learning/exam/2013/1108/v1097_241_1.gif) ≥2
≥2![\sqrt{16a^{3}.\sqrt[3]{abc}}](https://luyentap365.com/wp-content/picture/learning/exam/2013/1108/v1097_677_25.gif) = 8a.
= 8a.![\sqrt[6]{a^{4}bc}](https://luyentap365.com/wp-content/picture/learning/exam/2013/1108/v1097_774_26.gif)
≥ 8a![\sqrt[6]{b^{3}c^{3}}](https://luyentap365.com/wp-content/picture/learning/exam/2013/1108/v1097_234_27.gif) = 8a
= 8a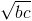 ≥ 3a
≥ 3a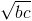 +3b
+3b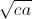 +2c
+2c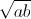
và ![\sqrt[3]{abc}^{2}](https://luyentap365.com/wp-content/picture/learning/exam/2013/1114/v1097_147947_23.gif) =
= ![\sqrt[3]{a^{2}b^{2}c^{2}}](https://luyentap365.com/wp-content/picture/learning/exam/2013/1108/v1097_864_33.gif) ≥ 8a
≥ 8a![\sqrt[3]{a^{\frac{3}{2}}b^{\frac{3}{2}}c^{3}}](https://luyentap365.com/wp-content/picture/learning/exam/2013/1108/v1097_169_34.gif) = c
= c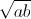
Cộng hai bất đẳng thức trên ta có điều phải chứng minh
Dấu đẳng thức xảy ra khi và chỉ khi a=b=c=
Câu hỏi liên quan
-

Tìm hệ số của x8 trong khai triển Niutơn của
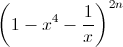 , biết rằng n thỏa mãn
, biết rằng n thỏa mãn 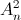 .
.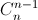 = 180. (
= 180. (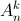 ,
, 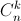 lần lượt là số chỉnh hợp, số tổ hợp chập k của n phần tử).
lần lượt là số chỉnh hợp, số tổ hợp chập k của n phần tử). -

Một hộp đựng 5 viên bi đỏ, 6 viên xanh và 7 viên bi vàng. Chọn ra 5 viên bi rừ hộp đó. Hỏi có bao nhiêu cách chọn mà 5 viên bi được chọn không có đủ cả 3 màu?
-

Trong không gian với hệ tọa độ Oxyz, cho hai đường thẳng d1:
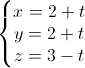 , d2:
, d2: 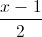 =
= 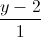 =
= 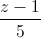 . Viết phương trình mặt phẳng song song và cách đều hai đường thẳng d1 và d2.
. Viết phương trình mặt phẳng song song và cách đều hai đường thẳng d1 và d2. -

Tìm số phức z thỏa mãn
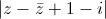 = √5 và (2 - z)(i +
= √5 và (2 - z)(i + 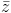 ) là số ảo.
) là số ảo. -

Trong không gian với hệ trục tọa độ Oxyz, viết phương trình đường thẳng ∆ nằm trong mặt phẳng (P): x+y-z+1=0, cắt các đường thẳng d:
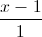 =
=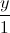 =
=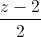 , d':
, d':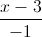 =
=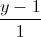 =
=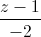 và tạo với đường thẳng d một góc
và tạo với đường thẳng d một góc 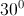 .
. -

Giải phương trình
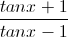 =
=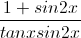
-

Trong mặt phẳng với hệ trục Oxy, cho hai đường thẳng ∆1: 3x+y+5=0, ∆2: x-2y-3=0 và đường tròn (C):
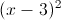 +
+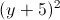 =25. Tìm điểm M thuộc (C), điểm N thuộc đường thẳng ∆1, sao cho M và N đối xứng qua ∆2.
=25. Tìm điểm M thuộc (C), điểm N thuộc đường thẳng ∆1, sao cho M và N đối xứng qua ∆2. -

Cho các số thực x, y, z không âm thỏa mãn điều kiện x3 + y3 + z3= 2 + 3xyz. Tìm giá trị nhỏ nhất của biểu thức P = x2 + 2y2 + 3z2.
-

Tìm số phức z thỏa mãn
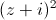 +
+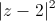 =2
=2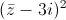 .
. -

Giải hệ phương trình
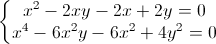 (x, y
(x, y R)
R)
