1. Giải phương trình: 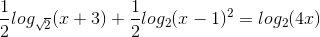 2. Cho phương trình:
2. Cho phương trình:
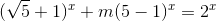 (với m là tham số)
Tìm m để phương trình có nghiệm thuộc đoạn [0,1]
(với m là tham số)
Tìm m để phương trình có nghiệm thuộc đoạn [0,1]

Câu hỏi
Nhận biết
1. Giải phương trình: 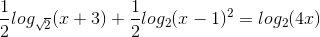
2. Cho phương trình:
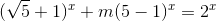 (với m là tham số)
(với m là tham số)
Tìm m để phương trình có nghiệm thuộc đoạn [0,1]
Đáp án đúng:
Lời giải của Luyện Tập 365
1. ĐKXĐ 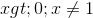
Pt (1) <=> ![log_{2}[(x+3)\left | x-1 \right |]=log_{2}4x\Leftrightarrow (x+3)\left | x-1 \right |=4x(2)](https://luyentap365.com/wp-content/picture/learning/exam/2014/1118/v61581_493819_2.gif)
0<x(x-3)(x-1)=4x <=>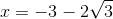 (loại) hoặc
(loại) hoặc 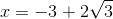 (TM).
(TM).
x>1 <=>(x-3)(x-1)=4x <=> x=-1(loại) hoặc x=3 (TM).
Kết luận; pt đã cho có hai nghiệm 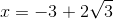 và
và 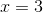
2. 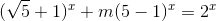 (1)
(1)
Chia cả hai vế của (1) cho 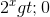 ta được pt (1) <=>
ta được pt (1) <=> 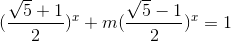
Đặt 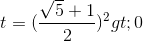 pt (2) trở thành:
pt (2) trở thành: 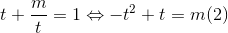 .
.
Khi ![x\epsilon [0;1]](https://luyentap365.com/wp-content/picture/learning/exam/2014/1118/v61581_182026_12.gif) thì
thì ![t\epsilon [1;\frac{\sqrt{5}+1}{2}]](https://luyentap365.com/wp-content/picture/learning/exam/2014/1118/v61581_402712_13.gif)
Pt (1) có nghiệm ![x\epsilon [0;1]](https://luyentap365.com/wp-content/picture/learning/exam/2014/1118/v61581_182026_12.gif) <=> pt (2) có nghiệm
<=> pt (2) có nghiệm ![t\epsilon [1;\frac{\sqrt{5}+1}{2}]](https://luyentap365.com/wp-content/picture/learning/exam/2014/1118/v61581_402712_13.gif) = K
= K
Xét hàm số 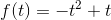 là hàm số liên tục trên R và có
là hàm số liên tục trên R và có 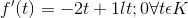
=> f(t) luôn nghịch biến trên K.pt (2) có nghiệm 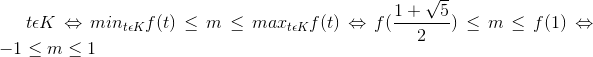
Vậy ![m\epsilon [-1;1]](https://luyentap365.com/wp-content/picture/learning/exam/2014/1118/v61581_62729_19.gif) thỏa mãn
thỏa mãn
1. ĐKXĐ 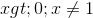
Pt (1) <=> ![log_{2}[(x+3)\left | x-1 \right |]=log_{2}4x\Leftrightarrow (x+3)\left | x-1 \right |=4x(2)](https://luyentap365.com/wp-content/picture/learning/exam/2014/1118/v61581_493819_2.gif)
0<x(x-3)(x-1)=4x <=>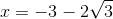 (loại) hoặc
(loại) hoặc 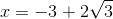 (TM).
(TM).
x>1 <=>(x-3)(x-1)=4x <=> x=-1(loại) hoặc x=3 (TM).
Kết luận; pt đã cho có hai nghiệm 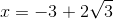 và
và 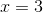
2. 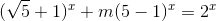 (1)
(1)
Chia cả hai vế của (1) cho 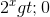 ta được pt (1) <=>
ta được pt (1) <=> 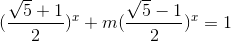
Đặt 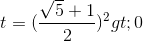 pt (2) trở thành:
pt (2) trở thành: 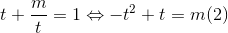 .
.
Khi ![x\epsilon [0;1]](https://luyentap365.com/wp-content/picture/learning/exam/2014/1118/v61581_182026_12.gif) thì
thì ![t\epsilon [1;\frac{\sqrt{5}+1}{2}]](https://luyentap365.com/wp-content/picture/learning/exam/2014/1118/v61581_402712_13.gif)
Pt (1) có nghiệm ![x\epsilon [0;1]](https://luyentap365.com/wp-content/picture/learning/exam/2014/1118/v61581_182026_12.gif) <=> pt (2) có nghiệm
<=> pt (2) có nghiệm ![t\epsilon [1;\frac{\sqrt{5}+1}{2}]](https://luyentap365.com/wp-content/picture/learning/exam/2014/1118/v61581_402712_13.gif) = K
= K
Xét hàm số 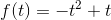 là hàm số liên tục trên R và có
là hàm số liên tục trên R và có 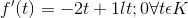
=> f(t) luôn nghịch biến trên K.pt (2) có nghiệm 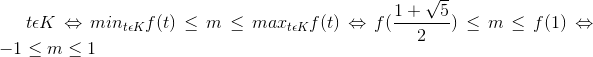
Vậy ![m\epsilon [-1;1]](https://luyentap365.com/wp-content/picture/learning/exam/2014/1118/v61581_62729_19.gif) thỏa mãn
thỏa mãn
Câu hỏi liên quan
-

Giải hệ phương trình
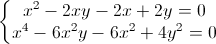 (x, y
(x, y R)
R) -

Giải phương trình (1-
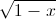 ).
).![\sqrt[3]{2-x}](https://luyentap365.com/wp-content/picture/learning/exam/2013/1031/75_220_2.gif) = x.
= x. -

Tìm hệ số của x8 trong khai triển Niutơn của
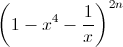 , biết rằng n thỏa mãn
, biết rằng n thỏa mãn 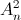 .
.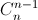 = 180. (
= 180. (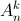 ,
, 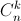 lần lượt là số chỉnh hợp, số tổ hợp chập k của n phần tử).
lần lượt là số chỉnh hợp, số tổ hợp chập k của n phần tử). -

Cho các số thực x, y, z không âm thỏa mãn điều kiện x3 + y3 + z3= 2 + 3xyz. Tìm giá trị nhỏ nhất của biểu thức P = x2 + 2y2 + 3z2.
-

Trong mặt phẳng với hệ trục Oxy, cho hình thoi ABCD biết phương trình của một đường chéo là 3x+y-7=0, điểm B(0;-3), diện tích hình thoi bằng 20. Tìm tọa độ các đỉnh còn lại của hình thoi.
-

Trong không gian với hệ tọa độ Oxyz, cho hai đường thẳng d1:
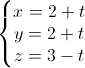 , d2:
, d2: 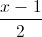 =
= 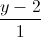 =
= 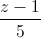 . Viết phương trình mặt phẳng song song và cách đều hai đường thẳng d1 và d2.
. Viết phương trình mặt phẳng song song và cách đều hai đường thẳng d1 và d2. -

Trong mặt phẳng với hệ trục Oxy, cho điểm M(4; -3) và đường tròn (C): x2 + y2 - 4x - 2y +1 = 0 với tâm là I. Lập phương trình tổng quát của đường thẳng d đi qua M và cắt đường tròn (C) tại hai điểm phân biệt P, Q sao cho tam giác IPQ vuông.
-

Tìm nghiệm trong khoảng(0, π) của phương trình
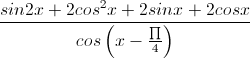 =
=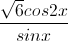
-

Tìm số phức z thỏa mãn
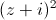 +
+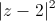 =2
=2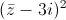 .
. -

Cho hàm số y =x3-6x2+3mx+2, với m là tham số thực. a) Khảo sát sự biến thiên và vẽ đồ thị của hàm số đã cho khi m=3 (HS tự làm). b) Tìm m sao cho đồ thị của hàm số đã cho có các điểm cực trị A,B thỏa mãn AB=4√65.
