Trong mặt phẳng với hệ toạ độ Oxy cho elip (E): 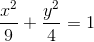 và hai điểm A(3;-2), B(-3;2). Tìm trên (E) điểm C có hoành độ và tung độ dương sao cho tam giác ABC có diện tích lớn nhất.
và hai điểm A(3;-2), B(-3;2). Tìm trên (E) điểm C có hoành độ và tung độ dương sao cho tam giác ABC có diện tích lớn nhất.

Câu hỏi
Nhận biếtTrong mặt phẳng với hệ toạ độ Oxy cho elip (E): 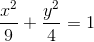 và hai điểm A(3;-2), B(-3;2). Tìm trên (E) điểm C có hoành độ và tung độ dương sao cho tam giác ABC có diện tích lớn nhất.
và hai điểm A(3;-2), B(-3;2). Tìm trên (E) điểm C có hoành độ và tung độ dương sao cho tam giác ABC có diện tích lớn nhất.
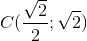
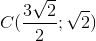
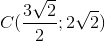
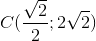
Đáp án đúng: B
Lời giải của Luyện Tập 365
Ta có PT đường thẳng AB:2x+3y=0
Gọi C(x;y) với x>0, y>0.
Diện tích tam giác ABC là:
SABC =  .AB.d(C;AB) =
.AB.d(C;AB) = 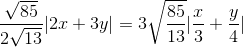
≤ 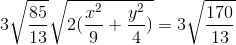
Dấu bẫng xảy ra khi: 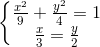 <=>
<=> 
Vậy 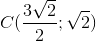
Ta có PT đường thẳng AB:2x+3y=0
Gọi C(x;y) với x>0, y>0.
Diện tích tam giác ABC là:
SABC =  .AB.d(C;AB) =
.AB.d(C;AB) = 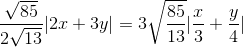
≤ 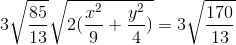
Dấu bẫng xảy ra khi: 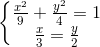 <=>
<=> 
Vậy 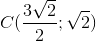
Câu hỏi liên quan
-

Cho các số thực x, y thỏa mãn điều kiện x+y=
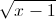 +
+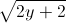 Tìm giá trị lớn nhất, giá trị nhỏ nhất của biểu thức
Tìm giá trị lớn nhất, giá trị nhỏ nhất của biểu thức
P=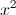 +
+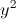 +2(x+1)(y+1)+8
+2(x+1)(y+1)+8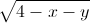
-

Trong mặt phẳng (P) cho tam giác đều ABC cạnh bằng a√6. Gọi M là trung điểm của AC và B' là điểm đối xứng với B qua M. Dựng điểm S sao cho SB' =3a và vuông góc với mặt phẳng (ABC). Gọi H là hình chiếu của M lên SB. Tính thể tích khối chóp H.ABC và góc giữa hai mặt phẳng (SAB) và (SBC).
-

Cho hàm số y =
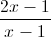 a) Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số. b) Tìm m để đường thẳng d : y = 3x+m cắt đồ thị (C) tại hai điểm A, B sao cho độ dài AB nhỏ nhất.
a) Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số. b) Tìm m để đường thẳng d : y = 3x+m cắt đồ thị (C) tại hai điểm A, B sao cho độ dài AB nhỏ nhất. -

Giải phương trình sin2x.(tan x - 1) = 3 sin x.(cos x + sin x) - 3.
-

Tìm hệ số của x8 trong khai triển Niutơn của
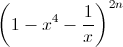 , biết rằng n thỏa mãn
, biết rằng n thỏa mãn 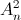 .
.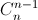 = 180. (
= 180. (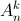 ,
, 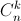 lần lượt là số chỉnh hợp, số tổ hợp chập k của n phần tử).
lần lượt là số chỉnh hợp, số tổ hợp chập k của n phần tử). -

Tính tích phân I =
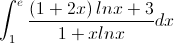
-

Trong mặt phẳng với hệ trục Oxy, cho điểm M(4; -3) và đường tròn (C): x2 + y2 - 4x - 2y +1 = 0 với tâm là I. Lập phương trình tổng quát của đường thẳng d đi qua M và cắt đường tròn (C) tại hai điểm phân biệt P, Q sao cho tam giác IPQ vuông.
-

Cho các số thực x,y thỏa mãn x
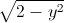 + y
+ y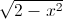 = 2 Tìm giá trị lớn nhất của biểu thức P=
= 2 Tìm giá trị lớn nhất của biểu thức P=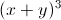 -12(x-1).(y-1)+√xy.
-12(x-1).(y-1)+√xy. -

Giải phương trình (1-
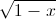 ).
).![\sqrt[3]{2-x}](https://luyentap365.com/wp-content/picture/learning/exam/2013/1031/75_220_2.gif) = x.
= x. -

Cho hình lập phương ABCD.A'B'C'D' có cạnh bằng a. Gọi O' là tâm của mặt đáy A'B'C'D', điểm M nằm trên đoạn thẳng BD sao cho BM=
 BD. Tính thể tích khối tứ diện ABMO' và khoảng cách giữa hai đường thẳng AM, O'D.
BD. Tính thể tích khối tứ diện ABMO' và khoảng cách giữa hai đường thẳng AM, O'D.
