Trong không gian với hệ tọa độ Oxyz, cho mặt cầu (S): (x - 1)2 + (y - 2)2 + (z - 3)2 = 9. Viết phương trình mặt phẳng (P) chứa trục Oy đồng thời cắt mặt cầu (S) theo một đường tròn có bán kính r = 2.

Câu hỏi
Nhận biếtTrong không gian với hệ tọa độ Oxyz, cho mặt cầu (S):
(x - 1)2 + (y - 2)2 + (z - 3)2 = 9. Viết phương trình mặt phẳng (P) chứa trục Oy đồng thời cắt mặt cầu (S) theo một đường tròn có bán kính r = 2.
 z = 0
z = 0  z = 0
z = 0  z = 0
z = 0 Đáp án đúng: B
Lời giải của Luyện Tập 365
(P) chứa trục Oy nên (P): Ax + Cz = 0, A2 + C2 > 0.
Gọi I(1; 2; 3), R = 3 là tâm và bán kính của mặt cầu (S)
Theo giả thiết ta có:
d(I,(P)) = 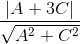 =
= 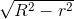 ⇔
⇔ 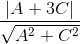 = √5
= √5
⇔ 4C2 + 6AC - 4A2 = 0
=> TH1
A = 2C , Chọn C =1 => A =2 => PT 2x+z=0
TH2 : A = -1/2.C chọn C =-2 => A =1 => Pt : x -2z =0
Vậy có hai mặt phẳng cần tìm là: x - 2z = 0 hoặc 2x +z =0
(P) chứa trục Oy nên (P): Ax + Cz = 0, A2 + C2 > 0.
Gọi I(1; 2; 3), R = 3 là tâm và bán kính của mặt cầu (S)
Theo giả thiết ta có:
d(I,(P)) = 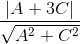 =
= 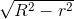 ⇔
⇔ 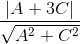 = √5
= √5
⇔ 4C2 + 6AC - 4A2 = 0
=> TH1
A = 2C , Chọn C =1 => A =2 => PT 2x+z=0
TH2 : A = -1/2.C chọn C =-2 => A =1 => Pt : x -2z =0
Vậy có hai mặt phẳng cần tìm là: x - 2z = 0 hoặc 2x +z =0
Câu hỏi liên quan
-

Cho các số thực x, y, z không âm thỏa mãn điều kiện x3 + y3 + z3= 2 + 3xyz. Tìm giá trị nhỏ nhất của biểu thức P = x2 + 2y2 + 3z2.
-

Trong không gian với hệ tọa độ Oxyz, cho hai mặt phẳng (α): 2x - y + z - 2 = 0, (β): x + 2y +2z - 4 = 0. Viết phương trình đường thẳng d nằm trong (α), song song với (β) và cách (β) một khoảng bằng 1.
-

Giải hệ phương trình
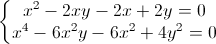 (x, y
(x, y R)
R) -

Tính tích phân I=
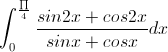
-

Trong không gian với hệ tọa độ Oxyz, cho hai đường thẳng d1:
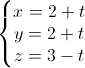 , d2:
, d2: 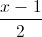 =
= 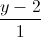 =
= 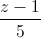 . Viết phương trình mặt phẳng song song và cách đều hai đường thẳng d1 và d2.
. Viết phương trình mặt phẳng song song và cách đều hai đường thẳng d1 và d2. -

Tính tích phân I =
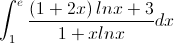
-

Trong không gian với hệ trục tọa độ Oxyz, viết phương trình đường thẳng ∆ nằm trong mặt phẳng (P): x+y-z+1=0, cắt các đường thẳng d:
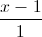 =
=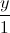 =
=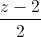 , d':
, d':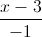 =
=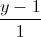 =
=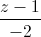 và tạo với đường thẳng d một góc
và tạo với đường thẳng d một góc 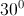 .
. -

Giải phương trình:
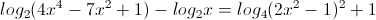
-

Trong mặt phẳng với hệ trục Oxy, cho tam giác ABC cân, cạnh đáy BC có phương trình x + y + 1 = 0. Phương trình đường cao vẽ từ B là x - 2y - 2 = 0. Điểm M(2; 1) thuộc đường cao vẽ từ C. Viết phương trình các cạnh bên của tam giác ABC.
-

Trong mặt phẳng với hệ trục Oxy, cho điểm M(4; -3) và đường tròn (C): x2 + y2 - 4x - 2y +1 = 0 với tâm là I. Lập phương trình tổng quát của đường thẳng d đi qua M và cắt đường tròn (C) tại hai điểm phân biệt P, Q sao cho tam giác IPQ vuông.
