Cho khai triển P(x) = (x3 + 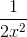 )n ta được
P(x) = a0x3n + a1x3n – 5 + a2x3n – 10 +......
Biết rằng 3 hệ số đầu a0, a1, a2 lập thành một cấp số cộng. Tính n và hệ số của số hạng chứa x4 trong khai triển trên.
)n ta được
P(x) = a0x3n + a1x3n – 5 + a2x3n – 10 +......
Biết rằng 3 hệ số đầu a0, a1, a2 lập thành một cấp số cộng. Tính n và hệ số của số hạng chứa x4 trong khai triển trên.

Câu hỏi
Nhận biếtCho khai triển P(x) = (x3 + 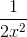 )n ta được
)n ta được
P(x) = a0x3n + a1x3n – 5 + a2x3n – 10 +......
Biết rằng 3 hệ số đầu a0, a1, a2 lập thành một cấp số cộng. Tính n và hệ số của số hạng chứa x4 trong khai triển trên.
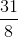
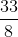
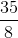
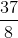
Đáp án đúng: C
Lời giải của Luyện Tập 365
(x3 + 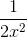 )n =
)n = 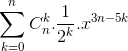
=> 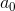 =
= 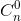 ,
, 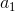 =
= 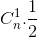 ;
; 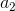 =
= 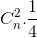
Theo giả thiết 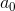 +
+ 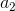 = 2
= 2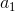 <=>
<=> 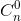 +
+ 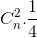 =
= 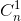 <=> n = 8
<=> n = 8
Gọi 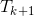 là số hạng tổng quát trong khai triển
là số hạng tổng quát trong khai triển
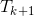 =
= 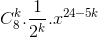 =>
=> 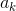 =
= 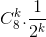
Giả sử 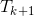 là số hạng chứa
là số hạng chứa 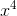 => 24 - 5k = 4 <=> k = 4
=> 24 - 5k = 4 <=> k = 4
Do đó hệ số của số hạng chứa 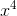 là
là 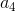 =
= 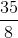
(x3 + 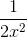 )n =
)n = 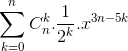
=> 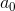 =
= 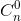 ,
, 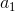 =
= 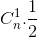 ;
; 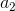 =
= 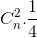
Theo giả thiết 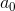 +
+ 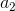 = 2
= 2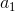 <=>
<=> 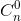 +
+ 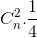 =
= 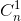 <=> n = 8
<=> n = 8
Gọi 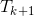 là số hạng tổng quát trong khai triển
là số hạng tổng quát trong khai triển
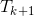 =
= 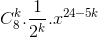 =>
=> 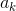 =
= 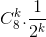
Giả sử 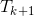 là số hạng chứa
là số hạng chứa 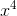 => 24 - 5k = 4 <=> k = 4
=> 24 - 5k = 4 <=> k = 4
Do đó hệ số của số hạng chứa 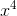 là
là 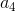 =
= 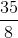
Câu hỏi liên quan
-

Cho hình chóp S.ABC có đáy là tam giác vuông cân tại B, BC = 2a. Gọi M là trung điểm của AC. Hình chiếu H của S lên mặt đáy (ABC) thuộc tia đối của tia MB sao cho MB = 2MH. Biết rằng góc giữa SA và mặt đáy (ABC) bằng 600. Tính thể tích khối chóp SABC và khoảng cách từ trung điểm E của SC tới (SAH).
-

Một hộp đựng 5 viên bi đỏ, 6 viên xanh và 7 viên bi vàng. Chọn ra 5 viên bi rừ hộp đó. Hỏi có bao nhiêu cách chọn mà 5 viên bi được chọn không có đủ cả 3 màu?
-

Tính tích phân I=
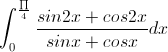
-

Cho các số thực x, y, z không âm thỏa mãn điều kiện x3 + y3 + z3= 2 + 3xyz. Tìm giá trị nhỏ nhất của biểu thức P = x2 + 2y2 + 3z2.
-

Giải phương trình (1-
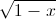 ).
).![\sqrt[3]{2-x}](https://luyentap365.com/wp-content/picture/learning/exam/2013/1031/75_220_2.gif) = x.
= x. -

Trong mặt phẳng với hệ trục Oxy, cho điểm M(4; -3) và đường tròn (C): x2 + y2 - 4x - 2y +1 = 0 với tâm là I. Lập phương trình tổng quát của đường thẳng d đi qua M và cắt đường tròn (C) tại hai điểm phân biệt P, Q sao cho tam giác IPQ vuông.
-

Trong không gian với hệ trục tọa độ Oxyz, viết phương trình đường thẳng ∆ nằm trong mặt phẳng (P): x+y-z+1=0, cắt các đường thẳng d:
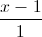 =
=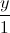 =
=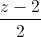 , d':
, d':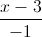 =
=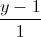 =
=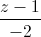 và tạo với đường thẳng d một góc
và tạo với đường thẳng d một góc 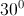 .
. -

Cho các số thực x, y thỏa mãn điều kiện x+y=
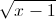 +
+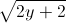 Tìm giá trị lớn nhất, giá trị nhỏ nhất của biểu thức
Tìm giá trị lớn nhất, giá trị nhỏ nhất của biểu thức
P=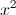 +
+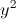 +2(x+1)(y+1)+8
+2(x+1)(y+1)+8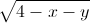
-

Trong không gian với hệ tọa độ Oxyz, cho hai đường thẳng d1:
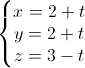 , d2:
, d2: 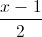 =
= 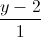 =
= 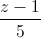 . Viết phương trình mặt phẳng song song và cách đều hai đường thẳng d1 và d2.
. Viết phương trình mặt phẳng song song và cách đều hai đường thẳng d1 và d2. -

Cho hàm số y =x3-6x2+3mx+2, với m là tham số thực. a) Khảo sát sự biến thiên và vẽ đồ thị của hàm số đã cho khi m=3 (HS tự làm). b) Tìm m sao cho đồ thị của hàm số đã cho có các điểm cực trị A,B thỏa mãn AB=4√65.
