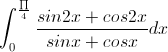Cho a, b,c > 0. Chứng minh rằng :
![\sqrt[3]{\frac{a}{b}}](https://luyentap365.com/wp-content/picture/learning/exam/2013/1129/6781_182314_1.gif) +
+ ![\sqrt[3]{\frac{b}{c}}](https://luyentap365.com/wp-content/picture/learning/exam/2013/1129/6781_545253_2.gif) +
+ ![\sqrt[3]{\frac{c}{a}}](https://luyentap365.com/wp-content/picture/learning/exam/2013/1129/6781_172899_3.gif) ≤
≤ ![\sqrt[3]{3(a+b+c)(\frac{1}{a}+\frac{1}{b}+\frac{1}{c})}](https://luyentap365.com/wp-content/picture/learning/exam/2013/1129/6781_724810_4.gif)

Câu hỏi
Nhận biếtCho a, b,c > 0. Chứng minh rằng :
![\sqrt[3]{\frac{a}{b}}](https://luyentap365.com/wp-content/picture/learning/exam/2013/1129/6781_182314_1.gif) +
+ ![\sqrt[3]{\frac{b}{c}}](https://luyentap365.com/wp-content/picture/learning/exam/2013/1129/6781_545253_2.gif) +
+ ![\sqrt[3]{\frac{c}{a}}](https://luyentap365.com/wp-content/picture/learning/exam/2013/1129/6781_172899_3.gif) ≤
≤ ![\sqrt[3]{3(a+b+c)(\frac{1}{a}+\frac{1}{b}+\frac{1}{c})}](https://luyentap365.com/wp-content/picture/learning/exam/2013/1129/6781_724810_4.gif)
Đáp án đúng: D
Lời giải của Luyện Tập 365
Ta chứng minh kết quả tổng quát sau : với t , u, v , m, n, p, x, y, z > 0 ta có ![\sqrt[3]{tuv}](https://luyentap365.com/wp-content/picture/learning/exam/2013/1129/v6778_581272_1.gif) +
+ ![\sqrt[3]{mnp}](https://luyentap365.com/wp-content/picture/learning/exam/2013/1129/v6778_790081_2.gif) +
+ ![\sqrt[3]{xyz}](https://luyentap365.com/wp-content/picture/learning/exam/2013/1129/v6778_644867_3.gif) ≤
≤ ![\sqrt[3]{(t+m+x)(u+n+y)(v+p+z)}](https://luyentap365.com/wp-content/picture/learning/exam/2013/1129/v6778_638182_4.gif) (**)
(**)
Thật vậy , theo bđt Cô – si ![\sqrt[3]{\frac{tuv}{(t+m+x)(u+n+y)(v+p+z)}}](https://luyentap365.com/wp-content/picture/learning/exam/2013/1129/v6778_504256_5.gif) ≤
≤ 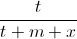 +
+ 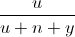 +
+ 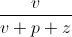 .
.
Viết hai bất đẳng thức tương tự rồi lấy tổng cả ba ta thu được 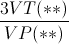 ≤ 3 => (**) đúng
≤ 3 => (**) đúng
Áp dụng bất đẳng thức này với t = m = x = 1, u = a, n = b, y = c, v = 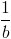 , p =
, p =  , z =
, z = 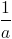 ta có ngay điều phải chứng minh. Dấu “ = “ xảy ra khi a = b =c = 1.
ta có ngay điều phải chứng minh. Dấu “ = “ xảy ra khi a = b =c = 1.
Ta chứng minh kết quả tổng quát sau : với t , u, v , m, n, p, x, y, z > 0 ta có ![\sqrt[3]{tuv}](https://luyentap365.com/wp-content/picture/learning/exam/2013/1129/v6778_581272_1.gif) +
+ ![\sqrt[3]{mnp}](https://luyentap365.com/wp-content/picture/learning/exam/2013/1129/v6778_790081_2.gif) +
+ ![\sqrt[3]{xyz}](https://luyentap365.com/wp-content/picture/learning/exam/2013/1129/v6778_644867_3.gif) ≤
≤ ![\sqrt[3]{(t+m+x)(u+n+y)(v+p+z)}](https://luyentap365.com/wp-content/picture/learning/exam/2013/1129/v6778_638182_4.gif) (**)
(**)
Thật vậy , theo bđt Cô – si ![\sqrt[3]{\frac{tuv}{(t+m+x)(u+n+y)(v+p+z)}}](https://luyentap365.com/wp-content/picture/learning/exam/2013/1129/v6778_504256_5.gif) ≤
≤ 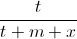 +
+ 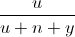 +
+ 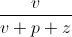 .
.
Viết hai bất đẳng thức tương tự rồi lấy tổng cả ba ta thu được 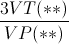 ≤ 3 => (**) đúng
≤ 3 => (**) đúng
Áp dụng bất đẳng thức này với t = m = x = 1, u = a, n = b, y = c, v = 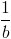 , p =
, p =  , z =
, z = 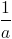 ta có ngay điều phải chứng minh. Dấu “ = “ xảy ra khi a = b =c = 1.
ta có ngay điều phải chứng minh. Dấu “ = “ xảy ra khi a = b =c = 1.
Câu hỏi liên quan
-

Giải phương trình sin2x.(tan x - 1) = 3 sin x.(cos x + sin x) - 3.
-

Trong không gian với hệ trục tọa độ Oxyz, viết phương trình đường thẳng ∆ nằm trong mặt phẳng (P): x+y-z+1=0, cắt các đường thẳng d:
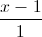 =
=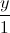 =
=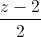 , d':
, d':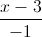 =
=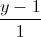 =
=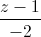 và tạo với đường thẳng d một góc
và tạo với đường thẳng d một góc 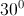 .
. -

Tìm hệ số của x8 trong khai triển Niutơn của
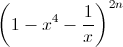 , biết rằng n thỏa mãn
, biết rằng n thỏa mãn 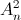 .
.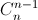 = 180. (
= 180. (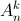 ,
, 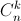 lần lượt là số chỉnh hợp, số tổ hợp chập k của n phần tử).
lần lượt là số chỉnh hợp, số tổ hợp chập k của n phần tử). -

Tìm số phức z thỏa mãn
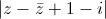 = √5 và (2 - z)(i +
= √5 và (2 - z)(i + 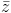 ) là số ảo.
) là số ảo. -

Tìm nghiệm trong khoảng(0, π) của phương trình
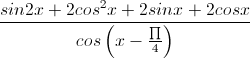 =
=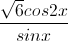
-

Giải phương trình
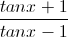 =
=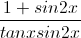
-

Tìm số phức z thỏa mãn
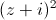 +
+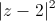 =2
=2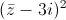 .
. -

Một hộp đựng 5 viên bi đỏ, 6 viên xanh và 7 viên bi vàng. Chọn ra 5 viên bi rừ hộp đó. Hỏi có bao nhiêu cách chọn mà 5 viên bi được chọn không có đủ cả 3 màu?
-

Trong mặt phẳng với hệ trục Oxy, cho tam giác ABC cân, cạnh đáy BC có phương trình x + y + 1 = 0. Phương trình đường cao vẽ từ B là x - 2y - 2 = 0. Điểm M(2; 1) thuộc đường cao vẽ từ C. Viết phương trình các cạnh bên của tam giác ABC.
-

Tính tích phân I=