Giải bất phương trình: 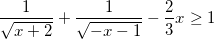 ; x∈R
; x∈R

Câu hỏi
Nhận biếtGiải bất phương trình: 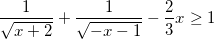 ; x∈R
; x∈R
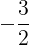
Đáp án đúng: C
Lời giải của Luyện Tập 365
Điều kiện: -2<x<-1
Với điều kiện (*) bất phương trình đã cho tương đương:
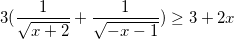
<=> 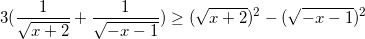
<=> 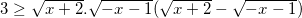 (1)
(1)
Đặt: t=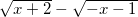 =>
=>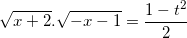
Bất phương trình (1) trở thành: 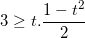 <=>
<=>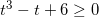
<=>(t+2)(t2-2t+3)≥0 <=> t ≥-2
Với t ≥ -2 ta có: 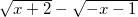 ≥ -2
≥ -2
<=>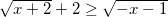
<=> x+6+4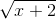 ≥ -x-1
≥ -x-1
<=>4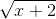 ≥ -(2x+7) (2)
≥ -(2x+7) (2)
Do -2 < x< -1
<=> 3< 2x+7 < 5
<=> -5< -(2x+7)<-3
Do đó: (2) thỏa mãn với mọi x thuộc tập xác định.
Vậy nghiệm của bất phương trình là: -2<x<-1
Điều kiện: -2<x<-1
Với điều kiện (*) bất phương trình đã cho tương đương:
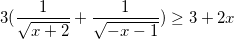
<=> 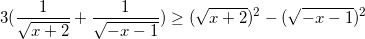
<=> 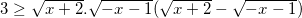 (1)
(1)
Đặt: t=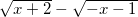 =>
=>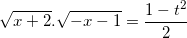
Bất phương trình (1) trở thành: 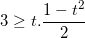 <=>
<=>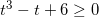
<=>(t+2)(t2-2t+3)≥0 <=> t ≥-2
Với t ≥ -2 ta có: 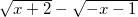 ≥ -2
≥ -2
<=>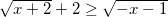
<=> x+6+4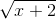 ≥ -x-1
≥ -x-1
<=>4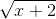 ≥ -(2x+7) (2)
≥ -(2x+7) (2)
Do -2 < x< -1
<=> 3< 2x+7 < 5
<=> -5< -(2x+7)<-3
Do đó: (2) thỏa mãn với mọi x thuộc tập xác định.
Vậy nghiệm của bất phương trình là: -2<x<-1
Câu hỏi liên quan
-

Cho hàm số y =
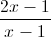 a) Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số. b) Tìm m để đường thẳng d : y = 3x+m cắt đồ thị (C) tại hai điểm A, B sao cho độ dài AB nhỏ nhất.
a) Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số. b) Tìm m để đường thẳng d : y = 3x+m cắt đồ thị (C) tại hai điểm A, B sao cho độ dài AB nhỏ nhất. -

Tìm hệ số của x8 trong khai triển Niutơn của
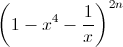 , biết rằng n thỏa mãn
, biết rằng n thỏa mãn 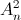 .
.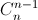 = 180. (
= 180. (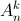 ,
, 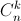 lần lượt là số chỉnh hợp, số tổ hợp chập k của n phần tử).
lần lượt là số chỉnh hợp, số tổ hợp chập k của n phần tử). -

Cho hình chóp S.ABC có đáy là tam giác vuông cân tại B, BC = 2a. Gọi M là trung điểm của AC. Hình chiếu H của S lên mặt đáy (ABC) thuộc tia đối của tia MB sao cho MB = 2MH. Biết rằng góc giữa SA và mặt đáy (ABC) bằng 600. Tính thể tích khối chóp SABC và khoảng cách từ trung điểm E của SC tới (SAH).
-

Cho các số thực x, y thỏa mãn điều kiện x+y=
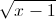 +
+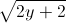 Tìm giá trị lớn nhất, giá trị nhỏ nhất của biểu thức
Tìm giá trị lớn nhất, giá trị nhỏ nhất của biểu thức
P=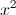 +
+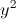 +2(x+1)(y+1)+8
+2(x+1)(y+1)+8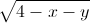
-

Trong không gian với hệ tọa độ Oxyz, cho hai đường thẳng d1:
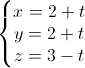 , d2:
, d2: 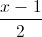 =
= 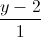 =
= 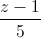 . Viết phương trình mặt phẳng song song và cách đều hai đường thẳng d1 và d2.
. Viết phương trình mặt phẳng song song và cách đều hai đường thẳng d1 và d2. -

Tìm số phức z thỏa mãn
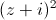 +
+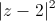 =2
=2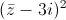 .
. -

Tính tích phân I =
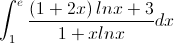
-

Trong mặt phẳng với hệ trục Oxy, cho hai đường thẳng ∆1: 3x+y+5=0, ∆2: x-2y-3=0 và đường tròn (C):
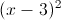 +
+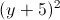 =25. Tìm điểm M thuộc (C), điểm N thuộc đường thẳng ∆1, sao cho M và N đối xứng qua ∆2.
=25. Tìm điểm M thuộc (C), điểm N thuộc đường thẳng ∆1, sao cho M và N đối xứng qua ∆2. -

Giải hệ phương trình
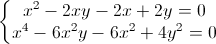 (x, y
(x, y R)
R) -

Trong không gian với hệ trục tọa độ Oxyz, viết phương trình đường thẳng ∆ nằm trong mặt phẳng (P): x+y-z+1=0, cắt các đường thẳng d:
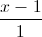 =
=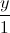 =
=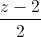 , d':
, d':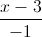 =
=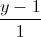 =
=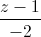 và tạo với đường thẳng d một góc
và tạo với đường thẳng d một góc 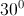 .
.
