Trong không gian tọa độ Oxyz cho đường thẳng ∆: 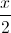 =
= 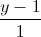 =
= 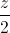 . Xác định tọa độ của điểm M trên trục hoành sao cho khoảng cách từ M đến ∆ bằng OM
. Xác định tọa độ của điểm M trên trục hoành sao cho khoảng cách từ M đến ∆ bằng OM

Câu hỏi
Nhận biếtTrong không gian tọa độ Oxyz cho đường thẳng ∆: 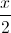 =
= 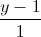 =
= 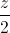 . Xác định tọa độ của điểm M trên trục hoành sao cho khoảng cách từ M đến ∆ bằng OM
. Xác định tọa độ của điểm M trên trục hoành sao cho khoảng cách từ M đến ∆ bằng OM
Đáp án đúng: C
Lời giải của Luyện Tập 365
d(M ; ∆) = 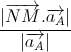 với M ∈ Ox ⇔ M(m ; 0 ; 0)
với M ∈ Ox ⇔ M(m ; 0 ; 0)
∆ qua N(0 ; 1 ; 0) có VTCP 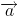 = (2 ; 1 ; 2)
= (2 ; 1 ; 2)
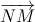 = (m ; -1 ; 0) ⇒ [
= (m ; -1 ; 0) ⇒ [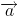 ;
; 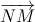 ] = (2 ; 2m ; -2 - m)
] = (2 ; 2m ; -2 - m)
Ta có: d(M ; ∆) = OM ⇔ ![\frac{|[\overrightarrow{a}.\overrightarrow{NM}]|}{|\overrightarrow{a}|}](https://luyentap365.com/wp-content/picture/learning/exam/2014/0822/v10563_995727_6.gif) = OM ⇔
= OM ⇔ 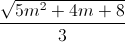 = |m|
= |m|
⇔ 4m2 – 4m – 8 = 0 ⇔ m = -1 hay m = 2. Vậy M(-1 ; 0 ; 0) hay M(2 ; 0 ; 0)
d(M ; ∆) = 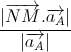 với M ∈ Ox ⇔ M(m ; 0 ; 0)
với M ∈ Ox ⇔ M(m ; 0 ; 0)
∆ qua N(0 ; 1 ; 0) có VTCP 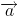 = (2 ; 1 ; 2)
= (2 ; 1 ; 2)
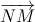 = (m ; -1 ; 0) ⇒ [
= (m ; -1 ; 0) ⇒ [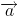 ;
; 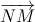 ] = (2 ; 2m ; -2 - m)
] = (2 ; 2m ; -2 - m)
Ta có: d(M ; ∆) = OM ⇔ ![\frac{|[\overrightarrow{a}.\overrightarrow{NM}]|}{|\overrightarrow{a}|}](https://luyentap365.com/wp-content/picture/learning/exam/2014/0822/v10563_995727_6.gif) = OM ⇔
= OM ⇔ 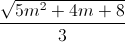 = |m|
= |m|
⇔ 4m2 – 4m – 8 = 0 ⇔ m = -1 hay m = 2. Vậy M(-1 ; 0 ; 0) hay M(2 ; 0 ; 0)
Câu hỏi liên quan
-

Trong mặt phẳng với hệ trục Oxy, cho tam giác ABC cân, cạnh đáy BC có phương trình x + y + 1 = 0. Phương trình đường cao vẽ từ B là x - 2y - 2 = 0. Điểm M(2; 1) thuộc đường cao vẽ từ C. Viết phương trình các cạnh bên của tam giác ABC.
-

Trong không gian với hệ tọa độ Oxyz, cho hai đường thẳng d1:
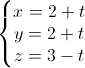 , d2:
, d2: 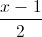 =
= 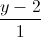 =
= 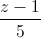 . Viết phương trình mặt phẳng song song và cách đều hai đường thẳng d1 và d2.
. Viết phương trình mặt phẳng song song và cách đều hai đường thẳng d1 và d2. -

Giải phương trình (1-
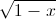 ).
).![\sqrt[3]{2-x}](https://luyentap365.com/wp-content/picture/learning/exam/2013/1031/75_220_2.gif) = x.
= x. -

Cho hàm số y =
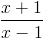 . a) Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số đã cho (HS tự làm). b) Tìm điểm M trên đồ thị (C) sao cho tổng khoảng cách từ M đến các đường thẳng ∆1: 2x + y - 4 = 0 và ∆2: x + 2y - 2 = 0 là nhỏ nhất.
. a) Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số đã cho (HS tự làm). b) Tìm điểm M trên đồ thị (C) sao cho tổng khoảng cách từ M đến các đường thẳng ∆1: 2x + y - 4 = 0 và ∆2: x + 2y - 2 = 0 là nhỏ nhất. -

Trong mặt phẳng với hệ trục Oxy, cho hình thoi ABCD biết phương trình của một đường chéo là 3x+y-7=0, điểm B(0;-3), diện tích hình thoi bằng 20. Tìm tọa độ các đỉnh còn lại của hình thoi.
-

Tính tích phân I=
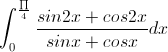
-

Tìm số phức z thỏa mãn
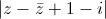 = √5 và (2 - z)(i +
= √5 và (2 - z)(i + 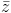 ) là số ảo.
) là số ảo. -

Tính tích phân I=
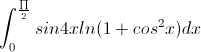
-

Giải phương trình sin2x.(tan x - 1) = 3 sin x.(cos x + sin x) - 3.
-

Cho các số thực x,y thỏa mãn x
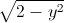 + y
+ y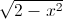 = 2 Tìm giá trị lớn nhất của biểu thức P=
= 2 Tìm giá trị lớn nhất của biểu thức P=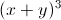 -12(x-1).(y-1)+√xy.
-12(x-1).(y-1)+√xy.
