Tìm số phức z thỏa mãn 2 điều kiện |z+1-2i|=|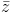 +3+4i| và \(w = \frac{{z - 2i}}{{\overline z + i}}\) là một số thuần ảo
+3+4i| và \(w = \frac{{z - 2i}}{{\overline z + i}}\) là một số thuần ảo

Câu hỏi
Nhận biếtTìm số phức z thỏa mãn 2 điều kiện |z+1-2i|=|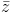 +3+4i| và \(w = \frac{{z - 2i}}{{\overline z + i}}\) là một số thuần ảo
+3+4i| và \(w = \frac{{z - 2i}}{{\overline z + i}}\) là một số thuần ảo
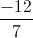 +
+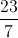 i
i  +
+ i
i 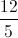 +
+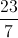 i
i Đáp án đúng: A
Lời giải của Luyện Tập 365
Giả sử \(z=x+yi\). Theo bài ra ta có \(|x+1+(y-2)i|=|x+3+(4-y)i|\)
\( \Leftrightarrow {\left( {x + 1} \right)^2} + {\left( {y - 2} \right)^2} = {\left( {x + 3} \right)^2} + {\left( {y - 4} \right)^2} \Leftrightarrow y = x + 5\)
Số phức
\(\begin{array}{l}w = \frac{{z - 2i}}{{z + i}} = \frac{{\left( {x + yi} \right) - 2i}}{{\left( {x - yi} \right) + i}}\\= \frac{{x + \left( {y - 2} \right)i}}{{x + \left( {1 - y} \right)i}} = \frac{{\left[ {x + \left( {y - 2} \right)i} \right]\left[ {x - \left( {1 - y} \right)i} \right]}}{{\left[ {x + \left( {1 - y} \right)i} \right]\left[ {x - \left( {1 - y} \right)i} \right]}}\\= \frac{{{x^2} + \left( {y - 2} \right)\left( {1 - y} \right) - x\left( {1 - y} \right)i + x\left( {y - 2} \right)i}}{{{x^2} + {{\left( {1 - y} \right)}^2}}}\\= \frac{{{x^2} - {y^2} + 3y - 2 + \left( {2xy - 3x} \right)i}}{{{x^2} + {{\left( {1 - y} \right)}^2}}}
\end{array}\)
w là số thuần ảo
\(\begin{array}{l}\left\{ \begin{array}{l}{x^2} - {y^2} + 3y - 2 = 0\\y = x + 5\end{array} \right.\\\Leftrightarrow \left\{ \begin{array}{l}{x^2} - {x^2} - 10x - 25 + 3x + 15 - 2 = 0\\y = x + 5\end{array} \right.\\\Rightarrow \left\{ \begin{array}{l}x = - \frac{{12}}{7}\\y = \frac{{23}}{7}\end{array} \right. \Rightarrow z = - \frac{{12}}{7} + \frac{{23}}{7}i\end{array}\)
Giả sử \(z=x+yi\). Theo bài ra ta có \(|x+1+(y-2)i|=|x+3+(4-y)i|\)
\( \Leftrightarrow {\left( {x + 1} \right)^2} + {\left( {y - 2} \right)^2} = {\left( {x + 3} \right)^2} + {\left( {y - 4} \right)^2} \Leftrightarrow y = x + 5\)
Số phức
\(\begin{array}{l}w = \frac{{z - 2i}}{{z + i}} = \frac{{\left( {x + yi} \right) - 2i}}{{\left( {x - yi} \right) + i}}\\= \frac{{x + \left( {y - 2} \right)i}}{{x + \left( {1 - y} \right)i}} = \frac{{\left[ {x + \left( {y - 2} \right)i} \right]\left[ {x - \left( {1 - y} \right)i} \right]}}{{\left[ {x + \left( {1 - y} \right)i} \right]\left[ {x - \left( {1 - y} \right)i} \right]}}\\= \frac{{{x^2} + \left( {y - 2} \right)\left( {1 - y} \right) - x\left( {1 - y} \right)i + x\left( {y - 2} \right)i}}{{{x^2} + {{\left( {1 - y} \right)}^2}}}\\= \frac{{{x^2} - {y^2} + 3y - 2 + \left( {2xy - 3x} \right)i}}{{{x^2} + {{\left( {1 - y} \right)}^2}}}
\end{array}\)
w là số thuần ảo
\(\begin{array}{l}\left\{ \begin{array}{l}{x^2} - {y^2} + 3y - 2 = 0\\y = x + 5\end{array} \right.\\\Leftrightarrow \left\{ \begin{array}{l}{x^2} - {x^2} - 10x - 25 + 3x + 15 - 2 = 0\\y = x + 5\end{array} \right.\\\Rightarrow \left\{ \begin{array}{l}x = - \frac{{12}}{7}\\y = \frac{{23}}{7}\end{array} \right. \Rightarrow z = - \frac{{12}}{7} + \frac{{23}}{7}i\end{array}\)
Câu hỏi liên quan
-

Trong mặt phẳng với hệ trục Oxy, cho hình thoi ABCD biết phương trình của một đường chéo là 3x+y-7=0, điểm B(0;-3), diện tích hình thoi bằng 20. Tìm tọa độ các đỉnh còn lại của hình thoi.
-

Tìm số phức z thỏa mãn
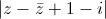 = √5 và (2 - z)(i +
= √5 và (2 - z)(i + 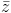 ) là số ảo.
) là số ảo. -

Giải phương trình
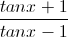 =
=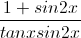
-

Tìm số phức z thỏa mãn
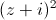 +
+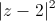 =2
=2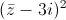 .
. -

Tính tích phân I=
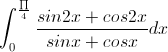
-

Cho các số thực x, y thỏa mãn điều kiện x+y=
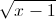 +
+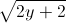 Tìm giá trị lớn nhất, giá trị nhỏ nhất của biểu thức
Tìm giá trị lớn nhất, giá trị nhỏ nhất của biểu thức
P=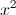 +
+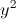 +2(x+1)(y+1)+8
+2(x+1)(y+1)+8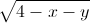
-

Cho hàm số y =x3-6x2+3mx+2, với m là tham số thực. a) Khảo sát sự biến thiên và vẽ đồ thị của hàm số đã cho khi m=3 (HS tự làm). b) Tìm m sao cho đồ thị của hàm số đã cho có các điểm cực trị A,B thỏa mãn AB=4√65.
-

Trong không gian với hệ tọa độ Oxyz, cho hai đường thẳng d1:
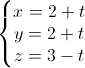 , d2:
, d2: 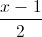 =
= 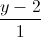 =
= 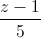 . Viết phương trình mặt phẳng song song và cách đều hai đường thẳng d1 và d2.
. Viết phương trình mặt phẳng song song và cách đều hai đường thẳng d1 và d2. -

Tìm nghiệm trong khoảng(0, π) của phương trình
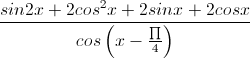 =
=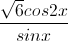
-

Cho hàm số y =
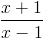 . a) Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số đã cho (HS tự làm). b) Tìm điểm M trên đồ thị (C) sao cho tổng khoảng cách từ M đến các đường thẳng ∆1: 2x + y - 4 = 0 và ∆2: x + 2y - 2 = 0 là nhỏ nhất.
. a) Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số đã cho (HS tự làm). b) Tìm điểm M trên đồ thị (C) sao cho tổng khoảng cách từ M đến các đường thẳng ∆1: 2x + y - 4 = 0 và ∆2: x + 2y - 2 = 0 là nhỏ nhất.
