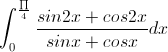Giải hệ phương trình: 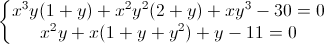

Câu hỏi
Nhận biếtGiải hệ phương trình: 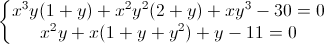
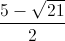 ;
;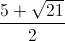 ), (
), (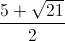 ;
;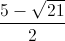 ).
).  ;
;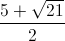 ), (
), (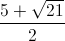 ;
; ).
). 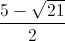 ;
;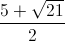 ), (
), (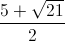 ;
;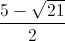 ).
). 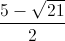 ;
;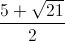 ), (
), (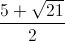 ;
;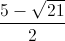 ).
). Đáp án đúng: A
Lời giải của Luyện Tập 365
+Hệ phương trình ⇔ 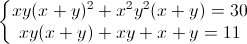
⇔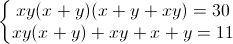
+Đặt x + y = u, xy = v, hệ trở thành:
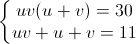 ⇔
⇔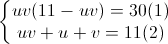
Từ (1)=>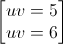
+Với uv = 5=> u + v = 6. Giải trường hợp này ta có nghiệm: (x , y) = (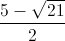 ;
;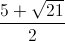 ), (
), (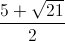 ;
;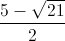 )
)
+Với uv = 6=>u + v = 5. Giải trường hợp này ta có nghiệm: (x , y) = (1,2), (2,1).
Kết luận: Hệ phương trình có 4 nghiệm: (x; y ) = (1;2), (2;1), (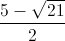 ;
;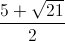 ), (
), (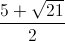 ;
;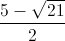 ).
).
+Hệ phương trình ⇔ 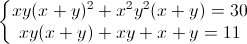
⇔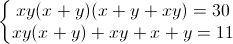
+Đặt x + y = u, xy = v, hệ trở thành:
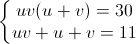 ⇔
⇔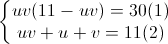
Từ (1)=>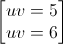
+Với uv = 5=> u + v = 6. Giải trường hợp này ta có nghiệm: (x , y) = (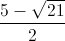 ;
;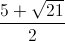 ), (
), (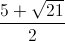 ;
;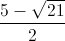 )
)
+Với uv = 6=>u + v = 5. Giải trường hợp này ta có nghiệm: (x , y) = (1,2), (2,1).
Kết luận: Hệ phương trình có 4 nghiệm: (x; y ) = (1;2), (2;1), (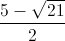 ;
;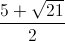 ), (
), (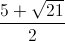 ;
;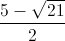 ).
).
Câu hỏi liên quan
-

Trong không gian với hệ tọa độ Oxyz, cho hai mặt phẳng (α): 2x - y + z - 2 = 0, (β): x + 2y +2z - 4 = 0. Viết phương trình đường thẳng d nằm trong (α), song song với (β) và cách (β) một khoảng bằng 1.
-

Cho các số thực x, y, z không âm thỏa mãn điều kiện x3 + y3 + z3= 2 + 3xyz. Tìm giá trị nhỏ nhất của biểu thức P = x2 + 2y2 + 3z2.
-

Trong không gian với hệ trục tọa độ Oxyz, viết phương trình đường thẳng ∆ nằm trong mặt phẳng (P): x+y-z+1=0, cắt các đường thẳng d:
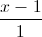 =
=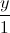 =
=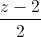 , d':
, d':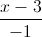 =
=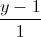 =
=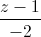 và tạo với đường thẳng d một góc
và tạo với đường thẳng d một góc 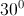 .
. -

Giải phương trình sin2x.(tan x - 1) = 3 sin x.(cos x + sin x) - 3.
-

Tính tích phân I =
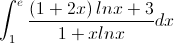
-

Cho các số thực x,y thỏa mãn x
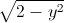 + y
+ y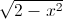 = 2 Tìm giá trị lớn nhất của biểu thức P=
= 2 Tìm giá trị lớn nhất của biểu thức P=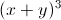 -12(x-1).(y-1)+√xy.
-12(x-1).(y-1)+√xy. -

Trong mặt phẳng với hệ trục Oxy, cho hình thoi ABCD biết phương trình của một đường chéo là 3x+y-7=0, điểm B(0;-3), diện tích hình thoi bằng 20. Tìm tọa độ các đỉnh còn lại của hình thoi.
-

Một hộp đựng 5 viên bi đỏ, 6 viên xanh và 7 viên bi vàng. Chọn ra 5 viên bi rừ hộp đó. Hỏi có bao nhiêu cách chọn mà 5 viên bi được chọn không có đủ cả 3 màu?
-

Giải phương trình
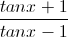 =
=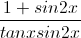
-

Tính tích phân I=