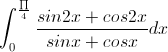Tìm giá trị lớn nhất và giá trị nhỏ nhất của hám sô 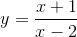 trên đoạn [-1,1]. Từ đó suy ra
trên đoạn [-1,1]. Từ đó suy ra 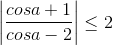 với mọi a
với mọi a
![Tìm giá trị lớn nhất và giá trị nhỏ nhất của hám sô trên đoạn [-1,1]. Từ đó suy ra với Tìm giá trị lớn nhất và giá trị nhỏ nhất của hám sô trên đoạn [-1,1]. Từ đó suy ra với](https://luyentap365.com/wp-content/themes/luyentap365/assets/images/tong-hop-cac-cau-hoi-on-tap-luyen-thi.png)
Câu hỏi
Nhận biếtTìm giá trị lớn nhất và giá trị nhỏ nhất của hám sô 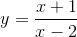 trên đoạn [-1,1]. Từ đó suy ra
trên đoạn [-1,1]. Từ đó suy ra 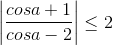 với mọi a
với mọi a
Đáp án đúng:
Lời giải của Luyện Tập 365
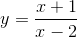
TXĐ D=[-1;1]
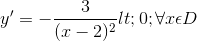
y(-1)=0; y(1)=-2
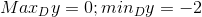
hay ![0\geq y\geq -2\forall x\epsilon D=[-1;1]](https://luyentap365.com/wp-content/picture/learning/exam/2014/1118/v61586_228665_4.gif)
đặt 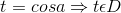 theo trên ta được
theo trên ta được
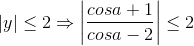
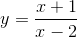
TXĐ D=[-1;1]
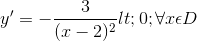
y(-1)=0; y(1)=-2
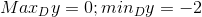
hay ![0\geq y\geq -2\forall x\epsilon D=[-1;1]](https://luyentap365.com/wp-content/picture/learning/exam/2014/1118/v61586_228665_4.gif)
đặt 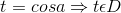 theo trên ta được
theo trên ta được
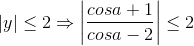
Câu hỏi liên quan
-

Trong mặt phẳng (P) cho tam giác đều ABC cạnh bằng a√6. Gọi M là trung điểm của AC và B' là điểm đối xứng với B qua M. Dựng điểm S sao cho SB' =3a và vuông góc với mặt phẳng (ABC). Gọi H là hình chiếu của M lên SB. Tính thể tích khối chóp H.ABC và góc giữa hai mặt phẳng (SAB) và (SBC).
-

Tìm số phức z thỏa mãn
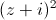 +
+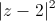 =2
=2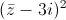 .
. -

Tính tích phân I=
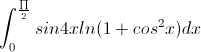
-

Giải phương trình
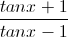 =
=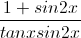
-

Giải phương trình:
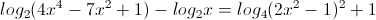
-

Giải phương trình (1-
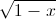 ).
).![\sqrt[3]{2-x}](https://luyentap365.com/wp-content/picture/learning/exam/2013/1031/75_220_2.gif) = x.
= x. -

Tính tích phân I =
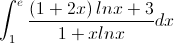
-

Tìm số phức z thỏa mãn
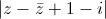 = √5 và (2 - z)(i +
= √5 và (2 - z)(i + 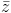 ) là số ảo.
) là số ảo. -

Giải phương trình sin2x.(tan x - 1) = 3 sin x.(cos x + sin x) - 3.
-

Tính tích phân I=