Trong không gian với hệ tọa độ Đề - các vuông góc Oxyz cho A( 3;0;0), B(1;2;1), C(2;-1;2). Gọi I là trung điểm của đoạn OA. Lập phương trình mặt phẳng (BIC)0. Chứng minh rằng với điểm M bất kì thuộc mặt phẳng (BIC) thì M luôn cách đều hai mặt phẳng ( OBC) và ( ABC)

Câu hỏi
Nhận biếtTrong không gian với hệ tọa độ Đề - các vuông góc Oxyz cho A( 3;0;0), B(1;2;1), C(2;-1;2). Gọi I là trung điểm của đoạn OA. Lập phương trình mặt phẳng (BIC)0. Chứng minh rằng với điểm M bất kì thuộc mặt phẳng (BIC) thì M luôn cách đều hai mặt phẳng ( OBC) và ( ABC)
Đáp án đúng: B
Lời giải của Luyện Tập 365
Vì I là trung điểm của OA nên tọa độ của I:
I( ; 0; 0) =>
; 0; 0) => 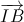 = (-
= (- ; 2 ;1);
; 2 ;1);
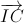 = (
= ( ; -1; 2) => [
; -1; 2) => [ 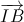 ;
; 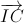 ] = (5;
] = (5;  ; -
; -  )
)
Ta chọn một vectơ pháp tuyến cho mặt phẳng (BIC) là: 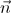 = ( 10;3;-1)
= ( 10;3;-1)
Vậy (BIC): 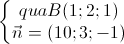
=>(BIC): 10(x – 1) + 3(y – 2) – 1(z – 1) = 0
⇔ 10x + 3y – z – 15 = 0.
Ta có : S∆ABC =  |[
|[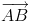 ,
,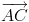 ]|; S∆OBC = |[
]|; S∆OBC = |[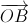 ,
,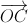 ]| và
]| và 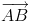 = (-2;2;1),
= (-2;2;1), 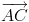 = ( -1;-1;2),
= ( -1;-1;2), 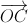 = (2;-1;2),
= (2;-1;2), 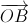 = (1;2;1).
= (1;2;1).
Từ đó dễ dàng ta có: S∆ABC = S∆OBC =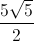
Theo giả thiết I là trung điểm của OA nên: d(O,(BIC)) = d(A,(BIC))
=>VOIBC = VAIBC=>d(I,(BOC)) = d(I,(BAC)) = h.
Nếu điểm M thuộc cạnh BC thì yêu cầu bài toán hiển nhiên.
d ( M,(BOC)) = d(M,(BAC)) = 0
Vì I là trung điểm của OA nên tọa độ của I:
I( ; 0; 0) =>
; 0; 0) => 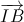 = (-
= (- ; 2 ;1);
; 2 ;1);
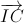 = (
= ( ; -1; 2) => [
; -1; 2) => [ 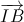 ;
; 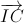 ] = (5;
] = (5;  ; -
; -  )
)
Ta chọn một vectơ pháp tuyến cho mặt phẳng (BIC) là: 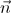 = ( 10;3;-1)
= ( 10;3;-1)
Vậy (BIC): 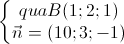
=>(BIC): 10(x – 1) + 3(y – 2) – 1(z – 1) = 0
⇔ 10x + 3y – z – 15 = 0.
Ta có : S∆ABC =  |[
|[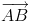 ,
,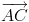 ]|; S∆OBC = |[
]|; S∆OBC = |[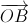 ,
,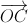 ]| và
]| và 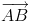 = (-2;2;1),
= (-2;2;1), 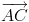 = ( -1;-1;2),
= ( -1;-1;2), 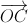 = (2;-1;2),
= (2;-1;2), 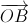 = (1;2;1).
= (1;2;1).
Từ đó dễ dàng ta có: S∆ABC = S∆OBC =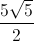
Theo giả thiết I là trung điểm của OA nên: d(O,(BIC)) = d(A,(BIC))
=>VOIBC = VAIBC=>d(I,(BOC)) = d(I,(BAC)) = h.
Nếu điểm M thuộc cạnh BC thì yêu cầu bài toán hiển nhiên.
d ( M,(BOC)) = d(M,(BAC)) = 0
Câu hỏi liên quan
-

Tính tích phân I =
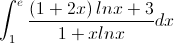
-

Tìm hệ số của x8 trong khai triển Niutơn của
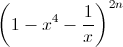 , biết rằng n thỏa mãn
, biết rằng n thỏa mãn 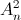 .
.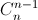 = 180. (
= 180. (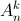 ,
, 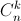 lần lượt là số chỉnh hợp, số tổ hợp chập k của n phần tử).
lần lượt là số chỉnh hợp, số tổ hợp chập k của n phần tử). -

Giải phương trình (1-
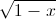 ).
).![\sqrt[3]{2-x}](https://luyentap365.com/wp-content/picture/learning/exam/2013/1031/75_220_2.gif) = x.
= x. -

Cho các số thực x, y thỏa mãn điều kiện x+y=
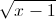 +
+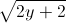 Tìm giá trị lớn nhất, giá trị nhỏ nhất của biểu thức
Tìm giá trị lớn nhất, giá trị nhỏ nhất của biểu thức
P=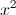 +
+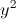 +2(x+1)(y+1)+8
+2(x+1)(y+1)+8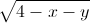
-

Trong không gian với hệ trục tọa độ Oxyz, viết phương trình đường thẳng ∆ nằm trong mặt phẳng (P): x+y-z+1=0, cắt các đường thẳng d:
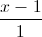 =
=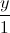 =
=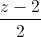 , d':
, d':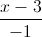 =
=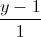 =
=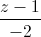 và tạo với đường thẳng d một góc
và tạo với đường thẳng d một góc 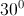 .
. -

Trong không gian với hệ tọa độ Oxyz, cho hai đường thẳng d1:
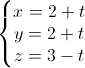 , d2:
, d2: 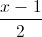 =
= 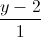 =
= 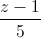 . Viết phương trình mặt phẳng song song và cách đều hai đường thẳng d1 và d2.
. Viết phương trình mặt phẳng song song và cách đều hai đường thẳng d1 và d2. -

Trong không gian với hệ tọa độ Oxyz, cho hai mặt phẳng (α): 2x - y + z - 2 = 0, (β): x + 2y +2z - 4 = 0. Viết phương trình đường thẳng d nằm trong (α), song song với (β) và cách (β) một khoảng bằng 1.
-

Một hộp đựng 5 viên bi đỏ, 6 viên xanh và 7 viên bi vàng. Chọn ra 5 viên bi rừ hộp đó. Hỏi có bao nhiêu cách chọn mà 5 viên bi được chọn không có đủ cả 3 màu?
-

Trong mặt phẳng với hệ trục Oxy, cho hai đường thẳng ∆1: 3x+y+5=0, ∆2: x-2y-3=0 và đường tròn (C):
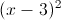 +
+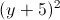 =25. Tìm điểm M thuộc (C), điểm N thuộc đường thẳng ∆1, sao cho M và N đối xứng qua ∆2.
=25. Tìm điểm M thuộc (C), điểm N thuộc đường thẳng ∆1, sao cho M và N đối xứng qua ∆2. -

Cho các số thực x, y, z không âm thỏa mãn điều kiện x3 + y3 + z3= 2 + 3xyz. Tìm giá trị nhỏ nhất của biểu thức P = x2 + 2y2 + 3z2.
