Giải hệ phương trình: ![\left\{\begin{matrix} x^{2}-3y+2+2\sqrt{x^2y+2y}=0\\\sqrt{x^2+4x-y+1} + \sqrt [3]{2x-1}=1 \end{matrix}\right.](https://luyentap365.com/wp-content/picture/learning/exam/2014/0004/15936_des_0.gif)

Câu hỏi
Nhận biếtGiải hệ phương trình: ![\left\{\begin{matrix} x^{2}-3y+2+2\sqrt{x^2y+2y}=0\\\sqrt{x^2+4x-y+1} + \sqrt [3]{2x-1}=1 \end{matrix}\right.](https://luyentap365.com/wp-content/picture/learning/exam/2014/0004/15936_des_0.gif)
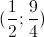
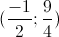
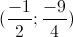
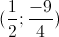
Đáp án đúng:
Lời giải của Luyện Tập 365
![\left\{\begin{matrix} x^{2}-3y+2+2\sqrt{x^2y+2y}=0 \(1)\\\sqrt{x^2+4x-y+1} + \sqrt [3]{2x-1}=1 \(2) \end{matrix}\right.](https://luyentap365.com/wp-content/picture/learning/exam/2014/0004/vip_15571_des_0.gif)
đk 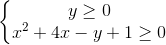
Ta có pt (1) <=> 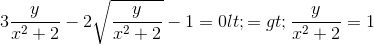
<=> y= x2 + 2 (3)
Thay (3) vào (2) ta được
![\sqrt{4x-1}+\sqrt[3]{2x-1}=1 (4)](https://luyentap365.com/wp-content/picture/learning/exam/2014/0004/vip_15571_des_3.gif)
Giải hệ pt(4) đặt ![\left\{\begin{matrix} u=\sqrt{4x-1}\\v=\sqrt[3]{2x-1} \end{matrix}\right.](https://luyentap365.com/wp-content/picture/learning/exam/2014/0004/vip_15571_des_4.gif) đk
đk 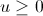 ta được hpt:
ta được hpt: 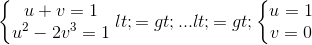
KL: Vậy hệ phương trình có nghiệm là 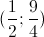
![\left\{\begin{matrix} x^{2}-3y+2+2\sqrt{x^2y+2y}=0 \(1)\\\sqrt{x^2+4x-y+1} + \sqrt [3]{2x-1}=1 \(2) \end{matrix}\right.](https://luyentap365.com/wp-content/picture/learning/exam/2014/0004/vip_15571_des_0.gif)
đk 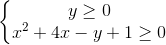
Ta có pt (1) <=> 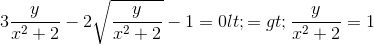
<=> y= x2 + 2 (3)
Thay (3) vào (2) ta được
![\sqrt{4x-1}+\sqrt[3]{2x-1}=1 (4)](https://luyentap365.com/wp-content/picture/learning/exam/2014/0004/vip_15571_des_3.gif)
Giải hệ pt(4) đặt ![\left\{\begin{matrix} u=\sqrt{4x-1}\\v=\sqrt[3]{2x-1} \end{matrix}\right.](https://luyentap365.com/wp-content/picture/learning/exam/2014/0004/vip_15571_des_4.gif) đk
đk 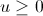 ta được hpt:
ta được hpt: 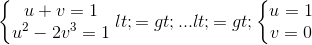
KL: Vậy hệ phương trình có nghiệm là 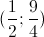
Câu hỏi liên quan
-

Cho các số thực x, y, z không âm thỏa mãn điều kiện x3 + y3 + z3= 2 + 3xyz. Tìm giá trị nhỏ nhất của biểu thức P = x2 + 2y2 + 3z2.
-

Trong không gian với hệ trục tọa độ Oxyz, viết phương trình đường thẳng ∆ nằm trong mặt phẳng (P): x+y-z+1=0, cắt các đường thẳng d:
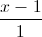 =
=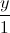 =
=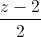 , d':
, d':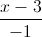 =
=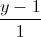 =
=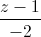 và tạo với đường thẳng d một góc
và tạo với đường thẳng d một góc 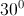 .
. -

Giải hệ phương trình
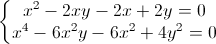 (x, y
(x, y R)
R) -

Tính tích phân I =
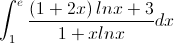
-

Tìm số phức z thỏa mãn
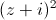 +
+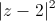 =2
=2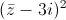 .
. -

Giải phương trình (1-
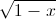 ).
).![\sqrt[3]{2-x}](https://luyentap365.com/wp-content/picture/learning/exam/2013/1031/75_220_2.gif) = x.
= x. -

Cho các số thực x,y thỏa mãn x
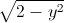 + y
+ y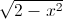 = 2 Tìm giá trị lớn nhất của biểu thức P=
= 2 Tìm giá trị lớn nhất của biểu thức P=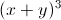 -12(x-1).(y-1)+√xy.
-12(x-1).(y-1)+√xy. -

Giải phương trình
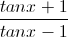 =
=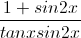
-

Cho hàm số y =
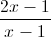 a) Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số. b) Tìm m để đường thẳng d : y = 3x+m cắt đồ thị (C) tại hai điểm A, B sao cho độ dài AB nhỏ nhất.
a) Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số. b) Tìm m để đường thẳng d : y = 3x+m cắt đồ thị (C) tại hai điểm A, B sao cho độ dài AB nhỏ nhất. -

Trong mặt phẳng với hệ trục Oxy, cho hai đường thẳng ∆1: 3x+y+5=0, ∆2: x-2y-3=0 và đường tròn (C):
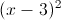 +
+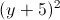 =25. Tìm điểm M thuộc (C), điểm N thuộc đường thẳng ∆1, sao cho M và N đối xứng qua ∆2.
=25. Tìm điểm M thuộc (C), điểm N thuộc đường thẳng ∆1, sao cho M và N đối xứng qua ∆2.
