Cho hình chóp S.ABCD có đáy ABCD là hình thoi tâm O; AC = 2a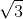 , BD = 2a; hai mặt phẳng (SAC) và (SBD) cùng vuông góc với mặt phẳng (ABCD). Biết khoảng cách từ điểm O đến mặt phẳng (SAB) bằng
, BD = 2a; hai mặt phẳng (SAC) và (SBD) cùng vuông góc với mặt phẳng (ABCD). Biết khoảng cách từ điểm O đến mặt phẳng (SAB) bằng 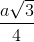 , tính thể tích khối chóp S.ABCD theo a.
, tính thể tích khối chóp S.ABCD theo a.

Câu hỏi
Nhận biếtCho hình chóp S.ABCD có đáy ABCD là hình thoi tâm O; AC = 2a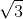 , BD = 2a; hai mặt phẳng (SAC) và (SBD) cùng vuông góc với mặt phẳng (ABCD). Biết khoảng cách từ điểm O đến mặt phẳng (SAB) bằng
, BD = 2a; hai mặt phẳng (SAC) và (SBD) cùng vuông góc với mặt phẳng (ABCD). Biết khoảng cách từ điểm O đến mặt phẳng (SAB) bằng 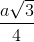 , tính thể tích khối chóp S.ABCD theo a.
, tính thể tích khối chóp S.ABCD theo a.
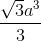
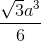
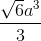
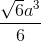
Đáp án đúng: A
Lời giải của Luyện Tập 365
Từ giả thiết AC = 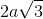 ; BD = 2a và AC, BD vuông góc với nhau tại trung điểm O của mỗi đường chéo. Ta có tam giác AOB vuông tại O và AO = a
; BD = 2a và AC, BD vuông góc với nhau tại trung điểm O của mỗi đường chéo. Ta có tam giác AOB vuông tại O và AO = a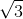 ; BO = a, do đó
; BO = a, do đó 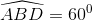

Hay tam giác ABD đều. Từ giả thiết hai mặt phẳng (SAC) và (SBD) cùng vuông góc với mặt phẳng (ABCD) nên giao tuyến của chúng là SO ⊥ (ABCD).
Do tam giác ABD đều nên với H là trung điểm của AB, K là trung điểm của HB ta có DH ⊥ AB và DH = a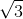 ;
;
OK // DH và OK =  DH =
DH = 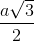
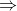 OK ⊥ AB
OK ⊥ AB 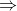 AB ⊥ (SOK)
AB ⊥ (SOK)
=> (SOK) vuông góc với (SAB); mà 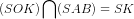
Gọi I là hình chiếu của O lên SK ta có OI ⊥ SK; AB⊥ OI 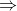 OI ⊥ (SAB), hay OI là khoảng cách từ O đến mặt phẳng (SAB).
OI ⊥ (SAB), hay OI là khoảng cách từ O đến mặt phẳng (SAB).
Tam giác SOK vuông tại O, OI là đường cao 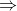
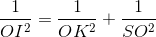
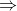 SO=
SO= 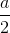
Diện tích đáy SABCD = 4S.∆ABO = 2.OA.OB=2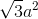 ;
;
đường cao của hình chóp 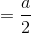 .
.
Thể tích khối chóp S.ABCD: 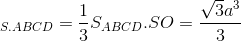 (đvtt)
(đvtt)
Từ giả thiết AC = 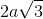 ; BD = 2a và AC, BD vuông góc với nhau tại trung điểm O của mỗi đường chéo. Ta có tam giác AOB vuông tại O và AO = a
; BD = 2a và AC, BD vuông góc với nhau tại trung điểm O của mỗi đường chéo. Ta có tam giác AOB vuông tại O và AO = a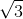 ; BO = a, do đó
; BO = a, do đó 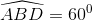

Hay tam giác ABD đều. Từ giả thiết hai mặt phẳng (SAC) và (SBD) cùng vuông góc với mặt phẳng (ABCD) nên giao tuyến của chúng là SO ⊥ (ABCD).
Do tam giác ABD đều nên với H là trung điểm của AB, K là trung điểm của HB ta có DH ⊥ AB và DH = a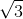 ;
;
OK // DH và OK =  DH =
DH = 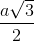
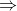 OK ⊥ AB
OK ⊥ AB 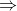 AB ⊥ (SOK)
AB ⊥ (SOK)
=> (SOK) vuông góc với (SAB); mà 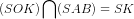
Gọi I là hình chiếu của O lên SK ta có OI ⊥ SK; AB⊥ OI 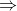 OI ⊥ (SAB), hay OI là khoảng cách từ O đến mặt phẳng (SAB).
OI ⊥ (SAB), hay OI là khoảng cách từ O đến mặt phẳng (SAB).
Tam giác SOK vuông tại O, OI là đường cao 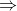
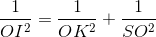
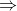 SO=
SO= 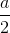
Diện tích đáy SABCD = 4S.∆ABO = 2.OA.OB=2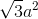 ;
;
đường cao của hình chóp 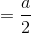 .
.
Thể tích khối chóp S.ABCD: 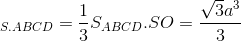 (đvtt)
(đvtt)
Câu hỏi liên quan
-

Cho các số thực x, y thỏa mãn điều kiện x+y=
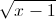 +
+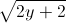 Tìm giá trị lớn nhất, giá trị nhỏ nhất của biểu thức
Tìm giá trị lớn nhất, giá trị nhỏ nhất của biểu thức
P=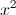 +
+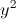 +2(x+1)(y+1)+8
+2(x+1)(y+1)+8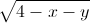
-

Trong không gian với hệ tọa độ Oxyz, cho hai đường thẳng d1:
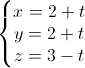 , d2:
, d2: 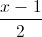 =
= 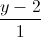 =
= 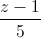 . Viết phương trình mặt phẳng song song và cách đều hai đường thẳng d1 và d2.
. Viết phương trình mặt phẳng song song và cách đều hai đường thẳng d1 và d2. -

Trong không gian với hệ trục tọa độ Oxyz, cho mặt phẳng (P) và đường thẳng d lần lượt có phương trình (P): 2x-y-2z=0, d:
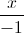 =
=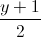 =
=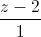 Viết phương trình mặt cầu (S) có tâm thuộc đường thẳng (d), cách mặt phẳng (P) một khoảng bằng 3 và cắt mặt phẳng (P) một khoảng bằng 3 và cắt mặt phẳng (P) theo giao tuyến là đường tròn có bán kính bằng 4.
Viết phương trình mặt cầu (S) có tâm thuộc đường thẳng (d), cách mặt phẳng (P) một khoảng bằng 3 và cắt mặt phẳng (P) một khoảng bằng 3 và cắt mặt phẳng (P) theo giao tuyến là đường tròn có bán kính bằng 4. -

Trong mặt phẳng với hệ trục Oxy, cho điểm M(4; -3) và đường tròn (C): x2 + y2 - 4x - 2y +1 = 0 với tâm là I. Lập phương trình tổng quát của đường thẳng d đi qua M và cắt đường tròn (C) tại hai điểm phân biệt P, Q sao cho tam giác IPQ vuông.
-

Trong không gian với hệ tọa độ Oxyz, cho hai mặt phẳng (α): 2x - y + z - 2 = 0, (β): x + 2y +2z - 4 = 0. Viết phương trình đường thẳng d nằm trong (α), song song với (β) và cách (β) một khoảng bằng 1.
-

Tính tích phân I =
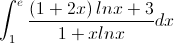
-

Tính tích phân I=
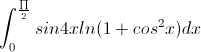
-

Giải phương trình:
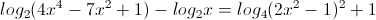
-

Một hộp đựng 5 viên bi đỏ, 6 viên xanh và 7 viên bi vàng. Chọn ra 5 viên bi rừ hộp đó. Hỏi có bao nhiêu cách chọn mà 5 viên bi được chọn không có đủ cả 3 màu?
-

Trong mặt phẳng với hệ trục Oxy, cho hình thoi ABCD biết phương trình của một đường chéo là 3x+y-7=0, điểm B(0;-3), diện tích hình thoi bằng 20. Tìm tọa độ các đỉnh còn lại của hình thoi.
