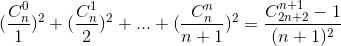Gọi X là tập hợp các số tự nhiên gồm năm chữ số đôi một khác nhau được tạo thành từ các chữ số 1,2,3,4,5,6,7,8,9. Chọn ngẫu nhiên mật số từ tập hợp X . Tính xác suất để số được chọn có tổng các chữ số là một số lẻ.
DANH SÁCH CÂU HỎI
-
[Gọi X là tập hợp các số tự nhiên gồm năm chữ số đôi một khác nhau được tạo thành từ các - Luyện Tập 365]
-
[Một hộp đựng 3 bi xanh , 4 bi đỏ và 5 bi vàng . Lấy ngẫu nhiên 5 bi từ hộp . Tính xác suất - Luyện Tập 365]
-
[Có 5 nhà toán học nam, 3 nhà toán học nữ, 4 nhà vật lý nam. Hỏi có bao nhiêu cách lập đoàn - Luyện Tập 365]
-
[Gọi S là tập hợp các số gồm 5 chữ số khác nhau 0,1,2,3,4,5,6,7. Lấy ngẫu nhiên 1 số tự nhiên - Luyện Tập 365]
-
[Trong khai triển đa thức: P(x) = Tìm hệ số của - Luyện Tập 365]
-
[Trong khai triển . Tìm số hạng không chứa x biết rằng: - Luyện Tập 365]
-
[(1.0 điểm) a) Cho số phức z thỏa mãn điều kiện z +(2 + i) = 3 + 5i . Tìm phần thực và phần - Luyện Tập 365]
-
[Gọi E là tập hợp các số tự nhiên gồm ba chữ số phân biệt được lập từ các chữ số 1, 2, 3, - Luyện Tập 365]
-
[Một hộp chứa 4 viên bi xanh, 3 viên bi đỏ và 2 viên bi vàng. Lấy ngẫu nhiên ra 2 viên bi. - Luyện Tập 365]
-
[Có bao nhiêu số tự nhiên chẵn gồm 4 chữ số đôi một khác nhau sao cho trong mỗi số đều có - Luyện Tập 365]
-
[Tìm hệ số x4trong khai triển (1+ x+ 2x2 )n, biết n là số nguyên dương thỏa mãn C02n+ - Luyện Tập 365]
-
[Cho số tự nhiên n ≥ 2, chứng minh đẳng thức - Luyện Tập 365]
-
[Gọi A là tập hợp tất cả các số tự nhiên gồm 5 chữ số phân biệt được chọn từ các chữ số 0; - Luyện Tập 365]
-
[Cho tập A = {0;1;2;3;4;5;6}. Xét các số tự nhiên có 5 chữ số khác nhau thuộc A . Trong các - Luyện Tập 365]
-
[Cho tập X = {0 ;1 ;2 ;3 ;4 ;5 ;6 ;7 }, S là tập hợp các số tự nhiên có 5 chữ số khác nhau - Luyện Tập 365]
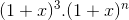
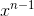
![(x.\sqrt[3]{x}+x^{-\frac{28}{15}})^{n}](https://luyentap365.com/wp-content/picture/learning/exam/2014/1219/74368_94142_1.gif)
. Tìm số hạng không chứa x biết rằng: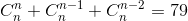 
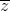= 3 + 5i . Tìm phần thực và phần ảo của z.