Cho số phức z thỏa mãn (1 + i)2.(2 – i)z = 8 + i + (1 + 2i)z . Tìm phần thực và phần ảo của z.
DANH SÁCH CÂU HỎI
-
[Cho số phức z thỏa mãn (1 + i)2.(2 – i)z = 8 + i + (1 + 2i)z - Luyện Tập 365]
-
[Giải phương trình: z2 – (1 + i)z + 6 + 3i = 0 trên tập hợp cá - Luyện Tập 365]
-
[Giải phương trình sau với ẩn 2 (z + - Luyện Tập 365]
-
[Giải phương trình : z3 + 3i.z2 – 3z + 7i = 0. - Luyện Tập 365]
-
[Giải phương trình : z4 + (2i – 3)z2 + 6i + 8 = 0 - Luyện Tập 365]
-
[Giải phương trình : z4 – 4z3 + 7z2 – 16 - Luyện Tập 365]
-
[Giải phương trình: z4 – 2z3 – z2 – 2z + - Luyện Tập 365]
-
[Giải phương trình: (z2 – z)(z2 + 5z + 6) = 10 - Luyện Tập 365]
-
[Giải phương trình: (z2 + 3z + 6)2 + 2z(z2 - Luyện Tập 365]
-
[Tìm số phức z thỏa mãn |z – (2 + i)| = √10 và z. - Luyện Tập 365]
-
[Tìm phần thực - phần ảo của số phức z = - Luyện Tập 365]
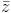)(1 + i) + (
+ 
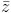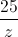= 8 – 6i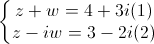
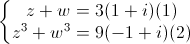
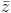= 25.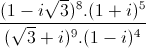
.