Trong các số phức z thỏa mãn điều kiện |z- 3- 3i| =√2, tìm số phức z có môđun nhỏ nhất
DANH SÁCH CÂU HỎI
-
[Trong các số phức z thỏa mãn điều kiện |z- 3- 3i| =√2, tìm số phức z có môđun nhỏ n - Luyện Tập 365]
-
[Giả sử z là số phức thỏa mãn z2 - 2z + 4 = 0. Tìm số phức W = - Luyện Tập 365]
-
[Tính môđun của số phức z biết (1 + 2i)z + (1- 2. - Luyện Tập 365]
-
[Tìm số phức z thỏa mãn (1 - 3i)z là số thực | - Luyện Tập 365]
-
[Tìm số phức z thoả mãn: |z - 2 + i| = 2. Biết phần ảo nhỏ hơn phần thực 3 đơn - Luyện Tập 365]
-
[Giải phương trình sau trên tập phức: z2 + 3(1+i)z – 6 – 13i = 0 - Luyện Tập 365]
-
[Cho số phức z thỏa mãn (1 – 2i)z - - Luyện Tập 365]
-
[Gọi z1, z2 là hai nghiệm phức của phương trình z2 - Luyện Tập 365]
-
[Cho số phức z thỏa mãn (2 + i)z + - Luyện Tập 365]
-
[Giải phương trình z2 + 3(1 + i)z + 5i = 0 trên tập hợp các - Luyện Tập 365]
-
[Cho số phức z thỏa mãn - Luyện Tập 365]
-
[Gọi z1 và z2 là hai nghiệm phức của phương trình z2 - Luyện Tập 365]
-
[Cho số phức z thỏa mãn điều kiện (2 – 3i)z + ( 4 + i) - Luyện Tập 365]
-
[Giải phương trình z2 – (1 + i)z + 6 + 3i = 0 trên tập hợp các số phức. - Luyện Tập 365]
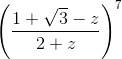
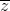)i = 1 + 3i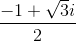 
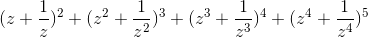
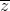- 2 + 5i| = 1 
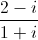= (3 – i)z. Tìm tọa độ điểm biểu diễn của z trong mặt phẳng tọa độ Oxy.
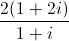= 7 + 8i. Tìm môđun của số phức w = z + 1 + i.
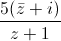= 2 – i. Tính môđun của số phức w = 1 + z + z2.
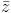= - (1 + 3i)2. Tìm phần thực và phần ảo của z.