Tìm tập hợp điểm M biểu diễn cho số phức z sao cho |z - 1 - 2i| = 2√2 (1). Từ đó hãy tìm số phức z thỏa mãn (1) sao cho phần ảo của z bằng 4.
DANH SÁCH CÂU HỎI
-
[Tìm tập hợp điểm M biểu diễn cho số phức z sao cho |z - 1 - 2i| = 2√2 (1). Từ đó hãy tìm - Luyện Tập 365]
-
[Trong mặt phẳng phức Oxy, tìm tập hợp các điểm M biểu diễn số phức w = (1 -2i)z + 3, biết - Luyện Tập 365]
-
[Tìm phần ảo của số phức w = iz + 4i biết rằng số phức z thỏa mãn phương trình = (1 - Luyện Tập 365]
-
[Giải phương trình sau trên tập số phức: (z2 + 3z + 6)2 + 2z(z2 + 3z + 6) - 3z2 = 0 - Luyện Tập 365]
-
[Tìm tập hợp những điểm biểu diễn số phức z sao cho w = là một số thực . - Luyện Tập 365]
-
[Tìm số phức z thỏa mãn: [(1 + i)z - 3].(2i - 3 + 2i) = 0 - Luyện Tập 365]
-
[Cho z1, z2 là các nghiệm phức của phương trình 2z2 – 4z + 11 = 0. Tính giá trị của biểu - Luyện Tập 365]
-
[Tìm môđun của số phức z - 2i biết (z - 2i).( - 2i) + 4iz = 0. - Luyện Tập 365]
-
[Tính modun của số phức z, biết z3 + 12i = , biết z có phần thực dương. - Luyện Tập 365]
-
[Tìm số phức z thỏa mãn điều kiện: 2|z|2 + 2 - Luyện Tập 365]
-
[Trong các số phức z thỏa mãn |z - 3i | = 1. Tìm số phức có mô đun nhỏ nhất.< - Luyện Tập 365]
-
[Tìm phần thực của số phức z = (1 + i)n , biết rằng: - Luyện Tập 365]
-
[Cho số phức Z1 - Luyện Tập 365]
-
[Tìm số phức z thỏa mãn (1 - 3i)z là số thực | - Luyện Tập 365]
-
[Tìm số phức z biết |z - 21|= 5 và iz + 3 là số ảo - Luyện Tập 365]
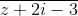= (1 + 2i)2(1 + z)
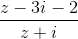là một số thực .
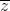- 3 + 2i) = 0
.
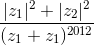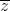- 2i) + 4iz = 0.
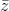, biết z có phần thực dương.
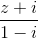= z.
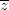+ 4(z +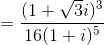 
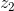, biết rằng 
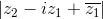= 2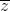
-2 + 5i| = 1