Tìm tất cả các số nguyên dương n sao cho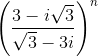 
là số thực .
DANH SÁCH CÂU HỎI
-
[Tìm tất cả các số nguyên dương n sao cho là số thực . - Luyện Tập 365]
-
[Xác định tập hợp các điểm M trên mặt phẳng phức biểu diễn số phức + 1 - i thỏa mãn - Luyện Tập 365]
-
[Giải phương trình sau trên tập số phức C: z4 – 2z3 – z2 - 2z + 1 = 0 - Luyện Tập 365]
-
[Tìm số phức z thỏa mãn điều kiện: z + 3 = (2 + i√3)|z| - Luyện Tập 365]
-
[Chứng minh số phức z với z = 1 + (1 + i√3) + (1 + i√3)2 + (1+ i√3)3 + …. + (1 + i√3)20 - Luyện Tập 365]
-
[Hãy tính tổng các số phức z thỏa mãn điều kiện z2 = │z│2 – 3 - Luyện Tập 365]
-
[Gọi z1, z2 là 2 nghiệm của phương trình z2 - (2cos)z + 1 = 0. Tìm số n nguyên dương nhỏ - Luyện Tập 365]
-
[Tìm modun của số phức w = b + ci (b, c ∈ R), biết số phức là nghiệm của phương trình - Luyện Tập 365]
-
[Gọi z1, z2 là các nghiệm phức của phương trình ()2 = -1 . Tìm giá trị biểu thức P = - Luyện Tập 365]
-
[Cho số phức z thỏa mãn điều kiện: có một acgumen bằng và │z│=│2 - √3 + i│. Tính - Luyện Tập 365]
-
[Cho số phức z thỏa mãn điều kiện: 1 + = | - i|2 + (iz – 1)2 . Tính mô đun của w = - Luyện Tập 365]
-
[Tìm số phức có modun nhỏ nhất sao cho: |z| = | - 3 + 4i| - Luyện Tập 365]
-
[Tìm môđun của số phức: w = 3 - zi + , biết (1 + i) - 1 - 3i = 0 . - Luyện Tập 365]
-
[Tính |z|, biết: z =(1 + i)(3 - 2i) - . - Luyện Tập 365]
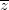+ 1 - i thỏa mãn log3|z - 1 + 2i| ≤ 1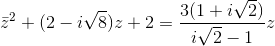
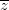= (2 + i√3)|z|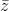
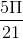)z + 1 = 0. Tìm số n nguyên dương nhỏ nhất sao cho z1n + z2n = 1.
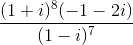là nghiệm của phương trình z2 + bz + c = 0
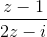)2 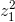= -1 .
)(1 +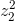 
) . 
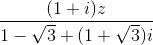có một acgumen bằng 
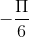và │z│=│2
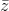- √3 + i│. Tính mô đun của số phức z .
= |
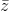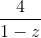
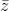- 3 + 4i|
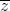, biết (1 + i)
.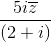