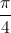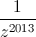Cho z1, z2 là các nghiệm của phương trình: 2z2-4z+11=0 trên tập số phức. Tính giá trị biểu thức: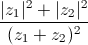 
.
DANH SÁCH CÂU HỎI
-
[Cho z1, z2 là các nghiệm của phương trình: 2z - Luyện Tập 365]
-
[Tìm số phức z thỏa mãn 2|z – i| = |2 + z - - Luyện Tập 365]
-
[Tìm số phức z sao cho |z -1| = |z -3| và một acgumen của z -3 bằng một a - Luyện Tập 365]
-
[Viết số phức z dưới dạng lượng giác biết rằng |z -1| = |z - √3i| và i - Luyện Tập 365]
-
[Cho số phức z thỏa mãn z2 – 6z + 13 =0. Tính |z + - Luyện Tập 365]
-
[Tìm số phức Z thỏa mãn |z - i| = √2 và (z - 1)( - Luyện Tập 365]
-
[Tìm tập hợp điểm trong mặt phẳng tọa độ biểu diễn số phức w = 2z + 3 - i - Luyện Tập 365]
-
[Cho số phức z1 ,z2 thỏa mãn điều kiện |z - Luyện Tập 365]
-
[Giả sửz1; z2là hai số phức thỏa mãn ph - Luyện Tập 365]
-
[Trong tất cả các số phức z thỏa mãn |z+1| = | - Luyện Tập 365]
-
[Trong tất cả các số phức z thỏa mãn - Luyện Tập 365]
-
[Tìm số phức z thỏa mãn |z - 3i| = |1 -i - Luyện Tập 365]
-
[Tìm số phức z thỏa mãn |1 - 2z| = |i - 2 - Luyện Tập 365]
-
[Cho số phức z thỏa mãn 2|z|+√3iz=4-z. Tính z2012+ - Luyện Tập 365]
-
[Giải phương trình sau trên tập hợp số phức z4 + 2z3 - Luyện Tập 365]
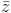| và 
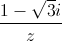có một acgumen là -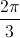 
.
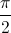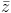có một acgumen là 
.
|
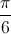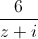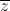+ i) là số thực
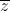+ 1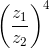
+ 
.
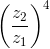. Tính môđun |z1 + z2|
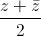+ 3|, hãy tìm số phức có môđun nhỏ nhất.
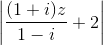= √3, hãy tìm số phức có mô đun nhỏ nhất và số phức có mô đun lớn nhất
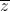| và z - 
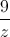là số ảo 
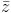| và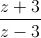 
có một acgumen bằng 
