Giải hệ phương trình: 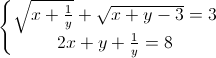 (x, y ∈R)
(x, y ∈R)
DANH SÁCH CÂU HỎI
-
[Giải hệ phương trình: - Luyện Tập 365]
-
[Tìm m ∈R để phương trình 2z2 + 2(m -1)z + 2m + 1 = 0 có hai n - Luyện Tập 365]
-
[Cho hệ phương trình - Luyện Tập 365]
-
[Cho phương trình √x + - Luyện Tập 365]
-
[Tìm tất cả các giá trị của a để phương trình sau có 3 nghiệm thực phân b - Luyện Tập 365]

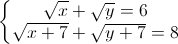
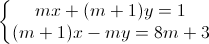 .Chứng tỏ rằng hệ luôn có cặp nghiệm duy nhất (x, y). Tìm m để biểu thức P = |x2 + y2 + (4 + 2√3)y| đạt giá trị lớn nhất.
.Chứng tỏ rằng hệ luôn có cặp nghiệm duy nhất (x, y). Tìm m để biểu thức P = |x2 + y2 + (4 + 2√3)y| đạt giá trị lớn nhất.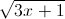 -
- 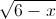 + 3x2 – 14x – 8 = 0 (x ∈
+ 3x2 – 14x – 8 = 0 (x ∈ 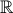 )
)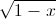 + 2m
+ 2m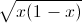 – 2
– 2![\sqrt[4]{x(1-x)}](https://luyentap365.com/wp-content/picture/learning/exam/2013/1212/10434_453979_3.gif) = m3 .Tìm m để phương trình có một nghiệm duy nhất.
= m3 .Tìm m để phương trình có một nghiệm duy nhất.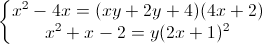 , (x, y ∈R)
, (x, y ∈R)![\left\{\begin{matrix}x^{2}+y^{2}-xy+4y+1=0\\y[7-(x-y)^{2}]=2(x^{2}+1)\end{matrix}\right.](https://luyentap365.com/wp-content/picture/learning/exam/2013/1212/10418_562845_1.gif)
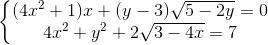 (x , y ∈
(x , y ∈ 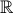 )
)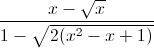 ≥ 1
≥ 1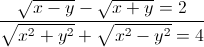
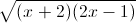 - 3
- 3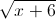 = 4 -
= 4 - 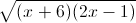 + 3
+ 3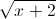
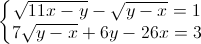
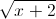 + x2 – x – 2 ≤
+ x2 – x – 2 ≤ 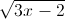 (x ∈
(x ∈ 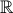 )
)