Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a,mặt bên SAB là tam giác đều, SC = a√2 . Gọi M là trung điểm của AD. Tính thể tích của khối chóp S.ABCD và khoảng cách giữa 2 đường thẳng CM và SD.
DANH SÁCH CÂU HỎI
-
[Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a,mặt bên SAB là tam giác đều, - Luyện Tập 365]
-
[Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh bằng a , tam giác SAC cân tại S - Luyện Tập 365]
-
[Cho hình chóp S.ABCD có đáy ABCD là hình thoi, 2 mặt phẳng (SAC) và (SBD) cùng vuôn - Luyện Tập 365]
-
[Cho lăng trụ đứng ABC.A'B'C' có đáy ABC là 1 tam giác vuông tại B, - Luyện Tập 365]
-
[Cho lăng trụ xiên ABC.A'B'C' có đáy là tâm giác vuông tại C: AB= 2a, cạnh bên AA'= - Luyện Tập 365]
-
[Trong mặp phẳng (P) cho hình vuông ABCD cạnh a. Trên các tia Ax, Cy cùng phía và vu - Luyện Tập 365]
-
[Cho hình chóp S.ABCD có đáy là hình bình hành với BA = a; BC = a√2, BD = a√5. Hình - Luyện Tập 365]
-
[Cho hình lăng trụ đều ABC.A'B'C' có đáy ABC là tam giác đều cạnh a. Gọi M là trung - Luyện Tập 365]
-
[Cho hình chóp S.ABCD có SA vuông góc với mặt phẳng (ABCD), SA=a, đáy ABCD là hình t - Luyện Tập 365]
-
[Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại A, - Luyện Tập 365]
-
[Cho hình chóp S. ABCD có đáy A - Luyện Tập 365]
-
[Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật AB = a, AD = 2√2. Hình chiế - Luyện Tập 365]
-
[Cho hình lăng trụ ABCD.A'B'C'D' có đáy ABCD là hình vuông cạnh a , c - Luyện Tập 365]
-
[Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật tâm I với AB = 2a√3 , BC = 2a. Bi - Luyện Tập 365]
-
[Trong mặt phẳng (P), cho hình thoi ABCD có độ dài các cạnh bằng a, - Luyện Tập 365]

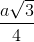 . Tính khoảng cách giữa CD,SA và tính thể tích khối chóp S.ABCD.
. Tính khoảng cách giữa CD,SA và tính thể tích khối chóp S.ABCD.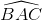 = 600.Bán kính đường tròn nội tiếp tam giác ABC bằng a và góc giữa 2 mặt phẳng (A'BC) và (ABC) bằng 600. Tính theo a thể tích khối lăng trụ ABC.A'B'C'
= 600.Bán kính đường tròn nội tiếp tam giác ABC bằng a và góc giữa 2 mặt phẳng (A'BC) và (ABC) bằng 600. Tính theo a thể tích khối lăng trụ ABC.A'B'C'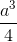
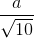 . Tính thể tích khối chóp S.ABCD theo a
. Tính thể tích khối chóp S.ABCD theo a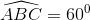 , BC=2a. Gọi H là điểm thuộc đoạn BC sao cho BC=4BH. Biết rằng SH vuông góc với mặt đáy (ABC) và SA tạo với mặt đáy một góc
, BC=2a. Gọi H là điểm thuộc đoạn BC sao cho BC=4BH. Biết rằng SH vuông góc với mặt đáy (ABC) và SA tạo với mặt đáy một góc 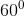 . Tính thể tích hình chóp S.ABC và chứng minh SC vuông góc với AD, trong đó D là điểm được xác định bởi
. Tính thể tích hình chóp S.ABC và chứng minh SC vuông góc với AD, trong đó D là điểm được xác định bởi 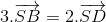 .
.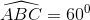 BC=2a. Gọi H là hình chiếu vuông góc của A trên BC. Biết rằng SH vuông góc với mặt đáy (ABC) và SA tạo với mặt đáy một góc 600. Tính thể tích khối chóp S.ABC và tính khoảng cách từ B đến mặt phẳng (SAC) theo a.
BC=2a. Gọi H là hình chiếu vuông góc của A trên BC. Biết rằng SH vuông góc với mặt đáy (ABC) và SA tạo với mặt đáy một góc 600. Tính thể tích khối chóp S.ABC và tính khoảng cách từ B đến mặt phẳng (SAC) theo a.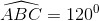 . Gọi G là trọng tâm tam giác ABD. Trên đường thẳng vuông góc với mặt phẳng (P) tại G lấy điểm S sao cho
. Gọi G là trọng tâm tam giác ABD. Trên đường thẳng vuông góc với mặt phẳng (P) tại G lấy điểm S sao cho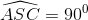 . Tính thể tích khối chóp SABCD và khoảng cách từ điểm G đến mặt phẳng (SBD) theo a.
. Tính thể tích khối chóp SABCD và khoảng cách từ điểm G đến mặt phẳng (SBD) theo a.