Cho hình chóp S.ABCD có đáy hình vuông cạnh a đường cao SA = a. Trên AB và AD lấy hai điểm M, N sao cho AM = DN = x (0 < x < a). Tính thể tích hình chóp S.AMCN theo a và x ? Xác định x để MN bé nhất.
DANH SÁCH CÂU HỎI
-
[Cho hình chóp S.ABCD có đáy hình vuông cạnh a đường cao SA = a. Trên AB và AD lấy hai điểm - Luyện Tập 365]
-
[Cho hình chóp S.ABCD có đáy ABCD là hình vuông. SA = a và vuông góc với mặt phẳng (ABC). - Luyện Tập 365]
-
[Cho lăng trụ đứng ABCD.A’B’C’D’ có đáy ABCD là hình thoi cạnh a, = 60o, AC' = 2a. Gọi - Luyện Tập 365]
-
[Cho hình lăng trụ đứng ABC.A’B’C’ có AB = a, AC = 2a, AA’ = 2a√5 và góc BAC = 1200. Gọi - Luyện Tập 365]
-
[Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật tâm O. SA vuông góc với đáy, SA = a, AB - Luyện Tập 365]
-
[Cho hình chóp S.ABCD có đáy ABCD là nửa lục giác đều nội tiếp đường tròn đường kính AD = - Luyện Tập 365]
-
[Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân đỉnh A, AB = a√2. Gọi I là trung điểm - Luyện Tập 365]
-
[Cho hình chóp S.ABCD có đáy ABCD là hình thoi, hai đường chéo AC = 2√3a , BD = 2a và cắt - Luyện Tập 365]
-
[Cho hình chóp S.ABCD đáy là hình vuông cạnh 2a, tam giác SAB đều, tam giác SCD vuông cân - Luyện Tập 365]
-
[Cho hình chóp S.ABC có SA = 3a (a > 0), SA tạo với đáy (ABC) góc 600. Tam giác ABC vuông - Luyện Tập 365]
-
[Cho hình chóp S.ABCD có SD vuông góc với mặt phẳng (ABCD), đáy ABCD là hình thoi cạnh a - Luyện Tập 365]
-
[Cho hình lăng trụ tam giác ABC.A'B'C' có AA' = 2a; AB = AC = a (a > 0) và góc giữa cạnh - Luyện Tập 365]
-
[Cho hình lăng trụ ABC.A1B1C1 có tất cả các cạnh bằ - Luyện Tập 365]
-
[Cho lăng trụ đứng ABC.A'B'C' có đáy là tam giác vuông tại B, AB = a, BC = 2a, - Luyện Tập 365]
-
[Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng a và cạnh bên bằng a - Luyện Tập 365]

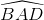 = 60o, AC' = 2a. Gọi O là giao điểm của BD và AC, E là giao điểm của A’O và AC’. Tính thể tích tứ diện EABD và khoảng cách từ A đến mặt phẳng (BDE).
= 60o, AC' = 2a. Gọi O là giao điểm của BD và AC, E là giao điểm của A’O và AC’. Tính thể tích tứ diện EABD và khoảng cách từ A đến mặt phẳng (BDE). 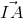 = -2
= -2 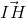 , góc giữa SC và mặt đáy (ABC) bằng 600. Hãy tính thế tich khối chóp S.ABC và khoảng cách từ trung điểm K của SB tới (SAH)
, góc giữa SC và mặt đáy (ABC) bằng 600. Hãy tính thế tich khối chóp S.ABC và khoảng cách từ trung điểm K của SB tới (SAH)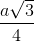 , tính thể tích khối chóp S.ABCD theo a, và góc giữa 2 mặt phẳng (SAB) với (SBD).
, tính thể tích khối chóp S.ABCD theo a, và góc giữa 2 mặt phẳng (SAB) với (SBD). 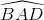 = 120o. Đường thẳng SA tạo với mặt phẳng (SBD) một góc bằng α với cotα = 3. Tính thể tích khối chóp S.ABCD và khoảng cách từ B đến mặt phẳng (SAC) theo a.
= 120o. Đường thẳng SA tạo với mặt phẳng (SBD) một góc bằng α với cotα = 3. Tính thể tích khối chóp S.ABCD và khoảng cách từ B đến mặt phẳng (SAC) theo a.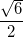 ; điểm M là trung điểm của cạnh SA. Tính thể tích tứ diện SMBD.
; điểm M là trung điểm của cạnh SA. Tính thể tích tứ diện SMBD.