Câu 1. Cho hình chóp S.ABCD có đáy là hình chữ nhật AB = a, BC = 2a; SA vuông góc với đáy, SA = a. Tính góc giữa 2 mặt phẳng (SBC) và (ABCD).
DANH SÁCH CÂU HỎI
-
[Câu 1. Cho hình chóp S.ABCD có đáy là hình chữ nhật AB = a, BC = 2a; SA vuông góc với đáy, - Luyện Tập 365]
-
[Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, tam giác SAB là tam giác đều và (SAB) - Luyện Tập 365]
-
[Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh bằng a. SA vuông góc với đáy, SA = . - Luyện Tập 365]
-
[Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại A, BC = 2a. Hình chiếu vuông góc - Luyện Tập 365]
-
[Cho hình lăng trụ ABCA'B'C', M' là trung điểm của AB, BC = 2a, , cạnh bên CC' tạo với mặt - Luyện Tập 365]
-
[Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại A, mặt been SBC là tam giác đểu - Luyện Tập 365]
-
[Cho tứ diện ABCD có AB = AC = a√2, BD = CD = a √3, BC = 2a, góc tạo bởi hai mặt phẳng (ABC) - Luyện Tập 365]
-
[Cho hình chóp S.ABCD có đáy là hình chữ nhật tâm I, AB = a, AD = 2a . Gọi M là trung điểm - Luyện Tập 365]
-
[Cho lăng trụ đều ABC.A'B'C ' có cạnh đáy bằng a , đường thẳng B'C tạo với đáy một góc 60o - Luyện Tập 365]
-
[Cho hình chóp đều S.ABC có SA = 6a, AB = 3a. Gọi M là điểm thuộc cạnh SC sao cho MS =MC. - Luyện Tập 365]
-
[Cho hình chóp S.ABC có đáy ABC và mặt bên SAB là những tam giác đều cạnh a. Mặt phẳng - Luyện Tập 365]
-
[Cho hình chóp S.ABCD có đáy ABCD là hình chứ nhật tâm O, cạnh AD=3a√2 và cạnh AB = 3a. - Luyện Tập 365]
-
[Trong không gian tọa độ Oxyz , cho điểm A(4;0;0) ; B(x0;y0;0) với x0;y0 là các số thực dương - Luyện Tập 365]
-
[Trong không gian tọa độ Oxyz , cho C(0;0;2); K(6;-3;0). Viết phương trình mặt phẳng (P) - Luyện Tập 365]
-
[Cho hình chóp S.ABCD có đáy ABCD là hình thoi, AB = 2a, = 600 . Hình chiếu vuônggóc - Luyện Tập 365]

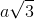 . Kẻ AH vuông góc với SB. Chứng minh rằng AH vuông góc với mặt phẳng (SBC) và tính
. Kẻ AH vuông góc với SB. Chứng minh rằng AH vuông góc với mặt phẳng (SBC) và tính 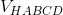
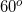 . Tính
. Tính 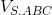
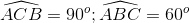 , cạnh bên CC' tạo với mặt phẳng (ABC) 1 góc
, cạnh bên CC' tạo với mặt phẳng (ABC) 1 góc 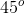
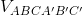
 MC. Tính thể tích của khối chóp S.ABC theo a và cosin của góc giữa hai đường thẳng SB và AM.
MC. Tính thể tích của khối chóp S.ABC theo a và cosin của góc giữa hai đường thẳng SB và AM. 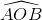 = 600. Xác định tọa độ điểm C trên trục Oz để thể tích tứ diện OABC bằng 8 .
= 600. Xác định tọa độ điểm C trên trục Oz để thể tích tứ diện OABC bằng 8 . 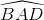 = 600 . Hình chiếu vuônggóc của đỉnh S lên mặt phẳng (ABCD) là trọng tâm H của tam giác ABD. Biết tam giác SAC vuông tại đỉnh S, tính thể tích khối chóp S.ABCD theo a và tính góc giữa hai mặt phẳng (SAC) và (SBC).
= 600 . Hình chiếu vuônggóc của đỉnh S lên mặt phẳng (ABCD) là trọng tâm H của tam giác ABD. Biết tam giác SAC vuông tại đỉnh S, tính thể tích khối chóp S.ABCD theo a và tính góc giữa hai mặt phẳng (SAC) và (SBC).