Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, tam giác SCD vuông tại S, góc 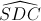 = 30o , hình chiếu của S xuống (ABCD) nằm trên cạnh CD. Gọi M là trung điểm của SA. Tính thể tích khối chóp MABD và góc giữa hai đường thẳng AC và DM.
= 30o , hình chiếu của S xuống (ABCD) nằm trên cạnh CD. Gọi M là trung điểm của SA. Tính thể tích khối chóp MABD và góc giữa hai đường thẳng AC và DM.
DANH SÁCH CÂU HỎI
-
[Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, tam giác SCD vuông tại - Luyện Tập 365]
-
[Cho hình lập phương ABCD.A'B'C'D' cạnh a. Gọi I,J,K lần lượt là trung đi - Luyện Tập 365]
-
[Cho hình lăng trụ ABC.A’B’C’ có cạnh bên AA’=2a - Luyện Tập 365]
-
[Cho hình chóp S.ABCD có đáy là hình thang vuông tại C và D, AD=3a, BC=CD - Luyện Tập 365]
-
[Cho hình chóp S.ABCD, có đáy ABCD là hình vuông cạnh bằng a, cạnh SA vuô - Luyện Tập 365]
-
[Cho lăng trụ ABC.A'B'C' có các cạnh bên là các hình vuông cạnh bằng a. G - Luyện Tập 365]
-
[Cho hình hộp chữ nhật ABCD.A'B'C'D'. Biết rằng góc giữa CA' và (ABCD) bằ - Luyện Tập 365]
-
[Cho hình lập phương ABCD.A'B'C'D' có cạnh bằng a. Gọi O' là tâm của mặt - Luyện Tập 365]

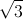 , AC=a , AB=BC=2a. Gọi M là trung điểm của BB’ . Biết rằng
, AC=a , AB=BC=2a. Gọi M là trung điểm của BB’ . Biết rằng 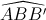 =
=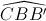 = 300 . Chứng minh rằng A'A⊥(MAC) và tính thể tích khối lăng trụ ABC.A’B’C’.
= 300 . Chứng minh rằng A'A⊥(MAC) và tính thể tích khối lăng trụ ABC.A’B’C’. BD. Tính thể tích khối tứ diện ABMO' và khoảng cách giữa hai đường thẳng AM, O'D.
BD. Tính thể tích khối tứ diện ABMO' và khoảng cách giữa hai đường thẳng AM, O'D.