Cho lăng trụ đứng ABCD.A'B'C'D' có đáy là hình thoi cạnh a, 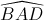
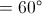 . Gọi M là trung điểm cạnh AA', N là trug điểm cạnh CC'. Chứng minh bốn điểm B', M, D, N cùng thuộc 1 mặt phẳng. Hãy tính độ dài cạnh AA' theo a để tứ giác B'MDN LÀ HÌNH VUÔNG.
. Gọi M là trung điểm cạnh AA', N là trug điểm cạnh CC'. Chứng minh bốn điểm B', M, D, N cùng thuộc 1 mặt phẳng. Hãy tính độ dài cạnh AA' theo a để tứ giác B'MDN LÀ HÌNH VUÔNG.
DANH SÁCH CÂU HỎI
-
[Cho lăng trụ đứng ABCD.A'B'C'D' có đáy là hình thoi cạnh a, - Luyện Tập 365]
-
[Cho hình chóp S.ABC có các cạnh SA, SB, SC đôi một vuông góc với nhau và - Luyện Tập 365]
-
[Cho lăng trụ đứng ABC.A1B1C1 có đáy ABC - Luyện Tập 365]
-
[Cho hình chóp S.ABC có SA = a, SB + SC = m ( m > 2a) - Luyện Tập 365]
-
[Cho hình chóp tứ giác đều SABCD; biết cạnh bên bằng 2a, góc giữa cạnh bê - Luyện Tập 365]
-
[Cho tứ diện ABCD có AB = x, các cạnh còn lại bằng nhau và bằng 1. Xác đị - Luyện Tập 365]
-
[Cho hình chóp S.ABCD có ABCD là hình chữ nhật: SA⊥ (ABCD); AB = SA - Luyện Tập 365]
-
[Cho tứ diện OABC có cạnh OA, OB, OC đôi một vuông góc với nhau và OA = O - Luyện Tập 365]
-
[Cho lăng trụ đứng ABC.A'B'C' có đáy là tam giác vuông tại A, AC = a,&nbs - Luyện Tập 365]
-
[Cho hình chóp SABC, đáy ABC là tam giác vuông cân đỉnh C ( - Luyện Tập 365]
-
[Cho hình lập phương ABCD.A1B1C1D1< - Luyện Tập 365]
-
[Cho hình hộp đứng ABCD.A’B’C’D’ có đáy là hình thoi cạnh a , góc g - Luyện Tập 365]
-
[Cho hình chóp tứ giác đều S.ABCD có đáy ABCD là hình vuông cạnh a. Gọi G - Luyện Tập 365]
-
[Cho tứ diện ABCD có AB = x, các cạnh còn lại bàng nhau và bằng 1. Xác đị - Luyện Tập 365]

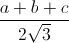
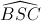 =
= 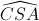 =
= 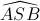 = 600 và
= 600 và 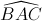 = 900 . Tính thể tích của khối chóp đã cho theo a và theo m.
= 900 . Tính thể tích của khối chóp đã cho theo a và theo m.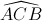 = 60o, Đường chéo BC' của mặt bên BB'C'C tạo với mặt đáy (ABC) một góc 30o. a, CMR tam giác ABC' vuông tại A. b, Tính thể tích khối lăng trụ ABC.A'B'C'
= 60o, Đường chéo BC' của mặt bên BB'C'C tạo với mặt đáy (ABC) một góc 30o. a, CMR tam giác ABC' vuông tại A. b, Tính thể tích khối lăng trụ ABC.A'B'C'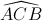 = 900). Cạnh bên SA của hình chóp vuông góc với mặt phẳng đáy và SC = a. Gọi góc giữa mặt phẳng (SBC) và (ABC) là α . Tìm α để thể tích hình chóp có giá trị lớn nhất.
= 900). Cạnh bên SA của hình chóp vuông góc với mặt phẳng đáy và SC = a. Gọi góc giữa mặt phẳng (SBC) và (ABC) là α . Tìm α để thể tích hình chóp có giá trị lớn nhất. 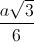 . Tính khoảng cách từ O đến (SCD), trong đó O là giao điểm của AC và BD. Tính thể tích của SABCD.
. Tính khoảng cách từ O đến (SCD), trong đó O là giao điểm của AC và BD. Tính thể tích của SABCD.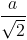 , hai đường tròn đáy là (O;a); (O';a). Điểm A thuộc đường tròn (O;a), điểm B thuộc đường tròn (O';a) sao cho AB=a. Tính thể tích của khối tứ diện OO'AB theo a.
, hai đường tròn đáy là (O;a); (O';a). Điểm A thuộc đường tròn (O;a), điểm B thuộc đường tròn (O';a) sao cho AB=a. Tính thể tích của khối tứ diện OO'AB theo a.