Cho hình lăng trụ đứng ABC.A’B’C’ có đáy là tam giác ABC cân tại C, cạnh đáy AB = 2a, cosABC = 
, góc giữa hai mặt phẳng ABC và A’BC bằng 600. Tính thể tích lăng trụ đứng ABC.A’B’C’ và khoảng cách giữa hai đường thẳng AB và BC’ theo a.
DANH SÁCH CÂU HỎI
-
[Cho hình lăng trụ đứng ABC.A’B’C’ có đáy là tam giác ABC cân tại C, cạnh - Luyện Tập 365]
-
[Cho một lăng trụ đứng ABC.A'B'C' có đáy ABC là tam giác cân đỉnh A, - Luyện Tập 365]
-
[Cho hình hộp ABCDA’B’C’D’ có các cạnh AB = AD = AA’ = 1 các góc phẳng tạ - Luyện Tập 365]
-
[Trong không gian Oxyz cho họ đường thẳng dKlà giao tuyế - Luyện Tập 365]
-
[Trong không gian, cho hình chóp S.ABCD có đáy ABCD là hình bình hành, AB - Luyện Tập 365]
-
[Cho lăng trụ xiên ABCA’B’C’ có đáy là tam giác đều cạnh a. Hình chiếu củ - Luyện Tập 365]
-
[Cho tam giác cân BMC có góc BMC = 1200 và đường cao MH = a√2. - Luyện Tập 365]
-
[Trong mặt phẳng (P) cho đường tròn (C) tâm O, đường kính AB = 2R. Cho O< - Luyện Tập 365]
-
[Cho hình chóp S.ABC có hình chiếu của đỉnh S lên mặt phẳng đáy nằm trong - Luyện Tập 365]
-
[Cho hình chóp tam giác đều SABC có cạnh đáy bằng a, cạnh bên 2a. Gọi I l - Luyện Tập 365]
-
[Cho A,B là biểu diễn hai nghiệm của pt: z2 + 6z + 18= 0 - Luyện Tập 365]
-
[Cho hình chóp SABC có đáy ABC là tam giác vuông tại B. SA vuông góc với - Luyện Tập 365]
-
[Tứ diện ABCD có cạnh AB=6, cạnh CD=8 và các cạnh còn lại bằng - Luyện Tập 365]
-
[Cho hình nón đỉnh S, đường cao SO. Cho A, B là hai điểm thuộc đường tròn - Luyện Tập 365]
-
[Cho hình chóp S.ABCD có thể tích bằng 18(đvtt), cạnh SD=6. Hãy tính độ d - Luyện Tập 365]
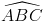=α, BC' hợp với đáy (ABC) một góc β. Gọi I là trung điểm của AA'. Biết rằng góc BIC là góc vuông 1. chứng tỏ rằng BIC là tam giác vuông cân (học sinh tự chứng minh) 2. Chứng minh rằng tan2α+tan2β=1
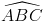=60o ,AB=4a, AC=2
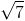a. Tính thể tích hình chóp S.ABC
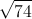. Hãy tính diện tích mặt cầu ngoại tiếp tứ diện ABCD
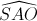= 300 , 
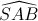= 600. Tính diện tích xung quanh của hình nón.