Cho hình chóp tú giác đều S.ABCD, đáy ABCD là hình vuông cạnh a, mặt bên nghiêng với đáy một góc 600. Một mặt phẳng (P) qua AB và vuông góc với mặt phẳng (SCD) cắt SC, SD lần lượt tại C’ và D’. Tính thể tích khối chóp S.ABC’D’
DANH SÁCH CÂU HỎI
-
[Cho hình chóp tú giác đều S.ABCD, đáy ABCD là hình vuông cạnh a, mặt bên - Luyện Tập 365]
-
[Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông ở A và B, góc BDC = - Luyện Tập 365]
-
[Cho lăng trụ tam giác đều ABCA’B’C’ có cạnh đáy bằng a. Gọi M, N lần lượ - Luyện Tập 365]
-
[Tính thể tích của hình chóp S.ABCD biết: SA = SB =SC =SD = AB = BC = CD - Luyện Tập 365]
-
[Cho hình hộp đứng ABCD.A'B'C'D' có AB = a, AD = 2a, AA' = 3a (a > 0) - Luyện Tập 365]
-
[Cho hình chóp tam giác đều S.ABC có cạnh đáy bằng a và cạnh bên tạo với - Luyện Tập 365]
-
[Cho hình chóp S.ABCD có đáy là hình chữ nhật , AB = a, BC = 2a, mặt bên - Luyện Tập 365]
-
[Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh bằng a và - Luyện Tập 365]
-
[Cho hình lăng trụ ABC.A'B'C' có đáy ABC là tam giác đều cạnh a, đỉnh A' - Luyện Tập 365]
-
[Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a, mặt bên (SBC) vuô - Luyện Tập 365]
-
[Cho lăng trụ đứng ABC.A’B’C’ có đáy ABC là tam giác vuông với AB = BC = - Luyện Tập 365]
-
[Trong không gian. Cho tam giác vuông cân ABC có cạnh huyền AB = 2a. Trên - Luyện Tập 365]
-
[Cho hình chóp S.ABCD có SA = x và tất cả các cạnh còn lại có độ dài bằng - Luyện Tập 365]
-
[Cho hình lăng trụ đứng ABC.A'B'C' có AC=a, BC=2a, góc ACB=120o - Luyện Tập 365]
-
[Cho hình chóp tứ giác đều S.ABCD có độ dài cạnh đáy bằng a, cạnh bên bằn - Luyện Tập 365]
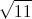, AB = a, SA = SB = SD = 2a. Tính thể tích của hình chóp S. ABD và khoảng cách từ S tới CD
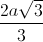, tính thể tích của hình chóp S.ABCD theo a
.
= 
.
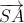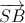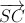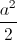Tính thể tích khối chóp S.ABC theo a.
= 
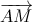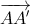. Tính thể tích khối tứ diện MA’BC’.
.
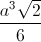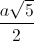. Tính góc tạo bởi mặt bên với mặt đáy và thể tích khối cầu ngoại tiếp hình chóp đó.