Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, cạnh bên SA vuông góc với mặt phẳng đáy, góc giữa mặt phẳng (SBD) và mặt phẳng đáy bằng 600 . Tính thể tích khối chóp S.ABCD theo a.
DANH SÁCH CÂU HỎI
-
[Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, cạnh bên SA vuông - Luyện Tập 365]
-
[Cho hình lăng trụ đứng ABC.A’B’C’ có đáy ABC là tam giác vuông tại B và - Luyện Tập 365]
-
[Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A và D với AD = - Luyện Tập 365]
-
[Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại B, AB = BC = 2a - Luyện Tập 365]
-
[Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, cạnh bên SA - Luyện Tập 365]
-
[Cho hình chóp S.ABCD đáy ABCD là hình vuông cạnh a, tam giác SAB cân tại - Luyện Tập 365]
-
[Cho lăng trụ đứng tam giác ABC.A’B’C’ biết A’A = AB = a, AC = 2a, góc BA - Luyện Tập 365]
-
[Cho lăng trụ đều ABC.A’B’C’ có tất cả các cạnh bằng a . Mặt phẳng (P) qu - Luyện Tập 365]
-
[Cho lăng trụ xiên ABC.A’B’C’ có đáy là tam giác đều cạnh a, cạnh bên AA’ - Luyện Tập 365]
-
[Cho hình lăng trụ tam giác đều ABC.A'B'C' có AB = a, góc giữa hai mặt ph - Luyện Tập 365]
-
[Cho một hình trụ tròn xoay và hình vuông ABCD cạnh a có hai đỉnh liên ti - Luyện Tập 365]
-
[Hình chóp S.ABCD có đáy ABCD là hình thoi, góc nhọn - Luyện Tập 365]
-
[Cho hình chóp SABCD có đáy ABCD là hình bình hành tâm O, AB = 2a, AD = 2 - Luyện Tập 365]
-
[Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a. Gọi M và N lần lư - Luyện Tập 365]
-
[Cho hình lập phương ABCD.A'B'C'D'. Một mặt phẳng (P) chia hình lập phươn - Luyện Tập 365]

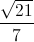 , tìm thể tích khối chóp S.MNP và tính diện tích mặt cầu ngoại tiếp hình chóp S.ABCD.
, tìm thể tích khối chóp S.MNP và tính diện tích mặt cầu ngoại tiếp hình chóp S.ABCD.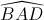 = α, bán kính đường tròn nội tiếp hình thoi là r , các bề mặt bên nghiêng đều trên đáy góc 600. Tính VS.ABCD .
= α, bán kính đường tròn nội tiếp hình thoi là r , các bề mặt bên nghiêng đều trên đáy góc 600. Tính VS.ABCD .