Cho hình chóp tam giác đều S.ABC với SA = 2a, AB = a. Gọi H là hình chiếu vuông góc của điểm A trên cạnh SC. Chứng minh SC vuông góc với mặt phẳng (ABH). Tính thể tích khối chóp S.ABH theo a.
DANH SÁCH CÂU HỎI
-
[Cho hình chóp tam giác đều S.ABC với SA = 2a, AB = a. Gọi H là hình chiế - Luyện Tập 365]
-
[Cho hình hộp đứng ABCD.A’B’C’D’ có đáy là hình vuông, tam giác A’AC vuôn - Luyện Tập 365]
-
[Cho hình chóp S.ABC có đáy ABC là một tam giác vuông cân AB = AC = a. Mặ - Luyện Tập 365]
-
[Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại B, AB = BC = 2a - Luyện Tập 365]
-
[Cho hình chóp tứ giác đều có cạnh đáy bằng a và chiều cao bằng h. Tính t - Luyện Tập 365]
-
[Cho lăng trụ ABCD.A1B1C1D1 c - Luyện Tập 365]
-
[Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân đỉnh B và SA⊥(ABC), - Luyện Tập 365]
-
[Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B, AB = 3a, BC = 4a - Luyện Tập 365]
-
[Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, mặt bên SAB là tam giá - Luyện Tập 365]
-
[Cho hình chóp S.ABCD có đáy là hình thoi cạnh a, cạnh bên SA vuông - Luyện Tập 365]
-
[Cho lăng trụ đều ABC.A’B’C’ có AB = a và đường thẳng A’B tạo với đáy một - Luyện Tập 365]
-
[Cho hình chóp S.ABC có đáy là tam giác vuông tại A, - Luyện Tập 365]
-
[Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B, BA = 3a, BC = 4a - Luyện Tập 365]
-
[Cho lăng trụ ABCD.A1B1C1D1 c - Luyện Tập 365]
-
[Cho hình chóp S.ABC có mặt bên SBC là tam giác đều cạnh a, cạnh bên SA v - Luyện Tập 365]

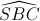 = 300. Tính thể tích khối chóp S.ABC và khoảng cách từ điểm B đến mặt phẳng (SAC) theo a.
= 300. Tính thể tích khối chóp S.ABC và khoảng cách từ điểm B đến mặt phẳng (SAC) theo a.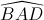 = 1200, M là trung điểm của cạnh BC và
= 1200, M là trung điểm của cạnh BC và 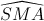 = 450. Tính theo a thể tích của khối chóp S.ABCD và khoảng cách từ điểm D đến mặt phẳng (SBC).
= 450. Tính theo a thể tích của khối chóp S.ABCD và khoảng cách từ điểm D đến mặt phẳng (SBC).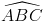 = 300, SBC là tam giác đều cạnh a và mặt bên SBC vuông góc với đáy. Tính theo a thể tích của khối chóp S.ABC và khoảng cách từ C đến mặt phẳng (SAB).
= 300, SBC là tam giác đều cạnh a và mặt bên SBC vuông góc với đáy. Tính theo a thể tích của khối chóp S.ABC và khoảng cách từ C đến mặt phẳng (SAB).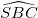 = 300. Tính thể tích khối chóp S.ABC và khoảng cách từ điểm B đến mặt phẳng (SAC) theo a
= 300. Tính thể tích khối chóp S.ABC và khoảng cách từ điểm B đến mặt phẳng (SAC) theo a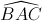 = 1200, tính thể tích của khối chóp S.ABC theo a.
= 1200, tính thể tích của khối chóp S.ABC theo a.