Cho hình chóp tam giác đều S.ABC với SA = 2a, AB = a. Gọi H là hình chiếu vuông góc của A trên cạnh SC. Chứng minh SC vuông góc với mặt phẳng (ABH). Tính thể tích của khối chóp S.ABH theo a.
DANH SÁCH CÂU HỎI
-
[Cho hình chóp tam giác đều S.ABC với SA = 2a, AB = a. Gọi H là hình chiếu vuô - Luyện Tập 365]
-
[Cho hình hộp đứng ABCD.A’BC’D’ có đáy là hình vuông, tam giác A’AC vuông cân, A’C = - Luyện Tập 365]
-
[Cho hình chóp S.ABC có đáy là tam giác đều cạnh a. Hình chiếu vuông góc của S trên - Luyện Tập 365]
-
[Cho hình chóp S.ABC có SA=3a (a>0); SA tạo với đáy (ABC) một góc bằng 60< - Luyện Tập 365]
-
[Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, mặt phẳng (SAB) vuông góc vớ - Luyện Tập 365]
-
[Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, cạnh bên SA = a; hình chiếu - Luyện Tập 365]
-
[Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại B, AB = a, SA vuông góc vớ - Luyện Tập 365]
-
[Cho hình chóp S.ABC có đáy là tam giác vuông cân tại C, cạnh huyền bằng 3a, G là tr - Luyện Tập 365]
-
[Cho hình lăng trụ đứng ABC. A'B'C' có đáy ABC là tam giác vuông tại B, AB = a, AA' - Luyện Tập 365]
-
[Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại A, 2AC=BC=2a. Mặt p - Luyện Tập 365]
-
[Cho hình hộp ABCD.A'B'C'D' có độ dài tất cả các cạnh bằng a>0 và góc - Luyện Tập 365]
-
[Cho hình lăng trụ tam giácABC.A'B'C' cóBB' = a, góc giữa đườ - Luyện Tập 365]
-
[Cho hình chóp tứ giác đềuS.ABCD cóAB = a, SA = a√2. Gọ - Luyện Tập 365]
-
[Cho hình chóp S.ABC có đáy là tam giác đều cạnh a, A' là trung điểm của - Luyện Tập 365]
-
[Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A và D, AB = AD - Luyện Tập 365]

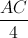 . Gọi CM là đường cao của tam giác SAC. Chứng minh M là trung điểm của SA và tính thể tích khối tứ diện SMBC theo a.
. Gọi CM là đường cao của tam giác SAC. Chứng minh M là trung điểm của SA và tính thể tích khối tứ diện SMBC theo a.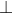 (ABC), SB=
(ABC), SB=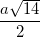 . Tính thể tích khối chóp S,ABC và khoảng cách từ B đến (SAC) theo a.
. Tính thể tích khối chóp S,ABC và khoảng cách từ B đến (SAC) theo a.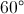 . Hình chiếu của S lên mặt phẳng (ABC) là trung điểm H của cạnh BC. Tính thể tích khối chóp S.ABC và khoảng cách giữa hai đường thẳng AH và SB.
. Hình chiếu của S lên mặt phẳng (ABC) là trung điểm H của cạnh BC. Tính thể tích khối chóp S.ABC và khoảng cách giữa hai đường thẳng AH và SB.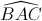 = 600. Hình chiếu vuông góc của điểm B' lên mặt phẳng ( ABC ) trùng với trọng tâm của tam giác ABC. Tính thể tích khối tứ diện A'ABC theo a.
= 600. Hình chiếu vuông góc của điểm B' lên mặt phẳng ( ABC ) trùng với trọng tâm của tam giác ABC. Tính thể tích khối tứ diện A'ABC theo a.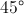 . Tính thể tích khối chóp S.ABC và góc giữa mặt bên (SAB) với mặt đáy theo a.
. Tính thể tích khối chóp S.ABC và góc giữa mặt bên (SAB) với mặt đáy theo a.