Trong không gian tọa độ Oxyz cho mặt cầu (S): x2 + y2 + z2 - 2x - 4y - 2z = 0 cắt các tia Ox, Oy, Oz lần lượt tại A, B, C khác O. Tìm tâm và bán kính đường tròn ngoại tiếp tam giác ABC.
DANH SÁCH CÂU HỎI
-
[Trong không gian tọa độ Oxyz cho mặt cầu (S): x2 + y2 + z2 - 2x - 4y - 2z = 0 cắt các tia - Luyện Tập 365]
-
[Trong không gian tọa độ Oxyz, cho mặt phẳng (P): x + 2y - z + 1 = 0 và điểm A(1; 1; 2). - Luyện Tập 365]
-
[Trong không gian với hệ trục tọa độ Oxyz, cho đường thẳng (∆): = = và - Luyện Tập 365]
-
[Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng (P) chứa đường thẳng d: = = và - Luyện Tập 365]
-
[Trong không gian với hệ tọa độ Oxyz cho các điểm A(1; 4; -3), B(4; 0; 1) và đường thẳng - Luyện Tập 365]
-
[Trong không gian với hệ tọa độ Oxyz cho tam giác ABC có A(1; 4; 3) và 2 đường thẳng ∆1: = = ; - Luyện Tập 365]
-
[Trong không gian với hệ tọa độ Oxyz, cho đường thẳng d: = = và - Luyện Tập 365]
-
[Trong không gian với hệ tọa độ Oxyz cho mặt phẳng (P): 2x + y + z - 2 = 0 và 2 đường thẳng - Luyện Tập 365]
-
[Trong không gian với hệ tọa độ Oxyz, cho hình vuông ABCD có A(5;3; -1), C(2;3; -4), B là - Luyện Tập 365]
-
[Trong không gian với hệ tọa độ Oxyz, cho các điểm B (-1;-4;-1); C(0;-2;-2); D(-1;-2 - Luyện Tập 365]
-
[Trong không gian tọa độ Oxyz, cho đường thẳng d: - Luyện Tập 365]
-
[Trong không gian Oxyz, cho hình chóp tam giác đều S.ABC biết A(3; 0; 0), B(0 - Luyện Tập 365]
-
[Trong không gian với hệ trục tọa độ Oxyz, viết phương trình mặt phẳng (P) đi qua O, - Luyện Tập 365]
-
[Trong không gian với hệ trục tọa độ Oxyz, cho (d): - Luyện Tập 365]
-
[Trong không gian với hệ trục tọa độ Oxyz cho điểm A(0; 1; 1), B(1; 0; -3), C(-1; -2 - Luyện Tập 365]
= 
= 
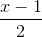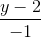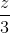và mặt phẳng (Q): 2x - y - 2z + 1 = 0. Tìm tọa độ các điểm thuộc đường thẳng (∆) mà khoảng cách từ đó đến mặt phẳng (Q) bằng 1.
= 
= 
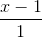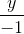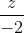và tạo với mặt phẳng (Q): 2x - 2y - z + 1 = 0 góc 600. Tìm tọa độ giao điểm M của mặt phẳng (P) với trục Oz.
= 
= 
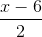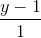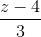. Xác định các điểm C, D sao cho ABCD là hình thoi biết rằng D nằm trên d.
= 
= 
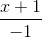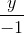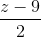; ∆2: 
= 
= 
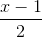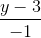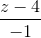lần lượt chứa đường trung tuyến kẻ từ đỉnh B và đường cao kẻ từ đỉnh C. Tìm tọa độ tâm và tính bán kính đường tròn ngoại tiếp tam giác ABC.
= 
= 
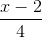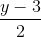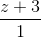và mặt phẳng (P): -x + y + 2z + 5 = 0. Viết phương trình đường thẳng ∆ nằm trong mặt phẳng (P), song song với d, và cách d một khoảng là √14.
= 
= 
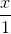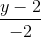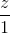, d2: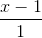 
= 
= 
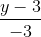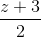. Viết phương trình đường thẳng ∆ song song với (P) đồng thời cẳ 2 đường thẳng d1, d2 lần lượt tạo M, N sao cho MN ngắn nhất.
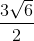AC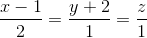
và mặt phẳng (P) có phương trình: x + 2y - z - 3 = 0. Viết phương trình đường thẳng ∆ thuộc (P), vuông góc với d và có khoảng cách giữa d và ∆ bằng √2
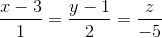, (d '): 
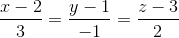và mặt phẳng (P): 2x + y + z −7 = 0. Đường thẳng ∆ cắt đường thẳng d và d’ tương ứng tại A và B đồng thời ∆ cách (P) một khoảng bằng √6. Viết phương trình đường thẳng ∆ ,biết rằng điểm A có hoành độ dương.