Trong không gian với hệ trục Oxyz, cho mặt cầu (S) có tâm I(1;–2;–1) và đi qua điểm A(3;–1; 1). Viết phương trình mặt phẳng (P) chứa trục Ox và cắt mặt cầu (S) theo giao tuyến là đường tròn có chu vi bằng 6π.
DANH SÁCH CÂU HỎI
-
[Trong không gian với hệ trục Oxyz, cho mặt cầu (S) có tâm I(1;–2;–1) và đi qua điểm A(3;–1; - Luyện Tập 365]
-
[Trong không gian Oxyz, cho tứ diện ABCD với A(2; 1; 0), B(1; 1; 3), C(2;-1; 3), D(1;-1;-0). - Luyện Tập 365]
-
[Trong không gian với hệ toạ độ Oxyz, cho mặt cầu (S) có phương trình: x2 + y2 + z2 - 2x - Luyện Tập 365]
-
[Trong không gian Oxyz cho điểm A(3;-2;-2) và mặt phẳng (P): x - y - z + 1 = 0. Viết phương - Luyện Tập 365]
-
[Trong không gian Oxyz, cho hai mặt phẳng (P): x - 2y + 2z - 2 = 0 và (Q): 2x + 2y + z - - Luyện Tập 365]
-
[Trong không gian Oxyz, cho mặt phẳng (P): x + 2y - 2z - 3 = 0, đường thẳng ∆: = = và - Luyện Tập 365]
-
[Trong không gian với hệ Oxyz cho 4 điểm A(1; 2; 3), B(-2; 2; -3), C(1; 1; -5), D(3; -1; - Luyện Tập 365]
-
[Trong không gian Oxyz, cho A(1; 0; 1); B(-1; 1; 1). Tìm tọa độ điểm M ∈ (Oxy) sao - Luyện Tập 365]
-
[Viết phương trình mặt phẳng (P) đi qua 2 điểm M(3; 0; 1); N(6; -2; 1) và tạo với mặt phẳng - Luyện Tập 365]
-
[Trong không gian với hệ tọa độ Oxyz, cho mặt cầu (S): (x - 1)2 + (y - 2)2 + (z - 3)2 = 9. - Luyện Tập 365]
-
[Trong không gian Oxyz cho điểm A(1; 1; 1). Viết phương trình mặt phẳng (P) qua gốc tọa độ - Luyện Tập 365]
-
[Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng (P): 3x + 2y - z + 4 = 0 và điểm A(2; - Luyện Tập 365]
-
[Trong không gian với hệ tọa độ Oxyz, cho mặt cầu(S): x2 + y2 + z2 - 2x + 6y – 4z + 5 = 0. - Luyện Tập 365]
-
[Trong không gian với hệ tọa độ Oxyz, cho điểm A(10;2;-1) và đường thẳng d: = - Luyện Tập 365]
-
[Trong không gian với hệ tọa độ Oxyz, cho 2 mặt phẳng (P): x + z – 3 = 0 và (Q): y + z + - Luyện Tập 365]
= 
= 
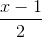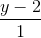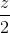và mặt cầu (S): x2 + y2 + z2 – 2x + 6y – 4z - 2 = 0. Hãy viết phương trình mặt phẳng (Q) song song với ∆, vuông góc với (P) và tiếp xúc với mặt cầu (S).
.
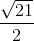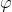thỏa mãn sin 
.
= 
= 
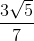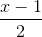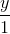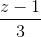. Lập phương trình mặt phẳng (P) đi qua A, song song và có khoảng cách từ d tới (P) là lớn nhất.