Trong không gian với hệ tọa độ Oxyz, cho đường thẳng d: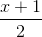 
= 
= 
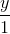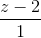mặt phẳng (P): x + y – 2z + 5 = 0 và điểm A(1; -1; 2). Viết phương trình đường thẳng ∆ cắt d và (P) lần lượt tại M và N sao cho A là trung điểm của đoạn MN.
DANH SÁCH CÂU HỎI
-
[Trong không gian với hệ tọa độ Oxyz, cho đường thẳng d: = = mặt phẳng - Luyện Tập 365]
-
[Trong không gian với hệ tọa độ Oxyz, cho đường thẳng d: = = và - Luyện Tập 365]
-
[Trong không gian với hệ trục tọa độ Oxyz, cho A(0; 1; 2), B(-1; 1; 0) và mặt phẳng (P): - Luyện Tập 365]
-
[Trong không gian với hệ trục tọa độ Oxyz, cho tam giác ABC có A(3; 1; 0), B nằm trên mặt - Luyện Tập 365]
-
[Trong không gian với hệ toạ độ Oxyz, cho hai đường thẳng (∆1): (t ∈ R) và (∆2): (s - Luyện Tập 365]
-
[Trong không gian tọa độ Oxyz, cho mặt cầu (S): x2+ y2 + z2 - 6x - 8y - 2z + 23 - Luyện Tập 365]
-
[Trong không gian tọa độ Oxyz, cho 3 điểm A(0; 1; 3), B(3; 0; -2), C(0; 2; 5) và mặt phẳng - Luyện Tập 365]
-
[Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng (P): x + 2y + 2z + 4 = 0 và mặt cầu - Luyện Tập 365]
-
[Trong không gian với hệ toạ độ Oxyz, cho điểm M(0; 1; 1) và 2 đường thẳng (d1), (d2) với - Luyện Tập 365]
-
[Trong không gian với hệ tọa độ Oxyz cho đường thẳng d: = = và mặt - Luyện Tập 365]
-
[Trong không gian với hệ tọa độ Oxyz, viết phương trình của mặt cầu (S) tiếp xúc với mặt - Luyện Tập 365]
-
[Trong không gian Oxyz cho mặt cầu (S): x2 + y2 + z2 - 2x + 2z – 2 =0 và các điểm A(0; 1; - Luyện Tập 365]
-
[Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng (P): x + 2y + z – 7 = 0 và các điểm A(2; - Luyện Tập 365]
-
[Trong không gian Oxyz cho mặt cầu (S): x2 + y2 + z2 - 2x + 2z - 2 = 0. Tìm điểm A thuộc - Luyện Tập 365]
-
[Trong không gian với hệ tọa độ Oxyz cho A(0; 0; 3), M(-2; - 3; -6). Điểm M’ thỏa mãn mặt - Luyện Tập 365]
= 
= 
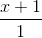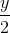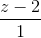và điểm I(0; 0; 3).
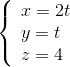(t ∈ R) và (∆2): 
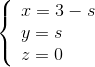(s ∈ R)
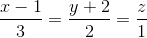và (d2):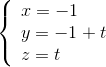 
= 
= 
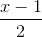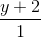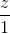và mặt phẳng (P): x + 2y – z - 3 = 0.
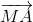- 2
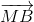+ 3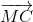
| đạt giá trị nhỏ nhất.