Trong không gian với hê tọa độ Oxyz, cho các điểm A (3 ; -1 ; 1), B (-1 ; 0 ; -2), C (4 ; 1; -1), D (3 ; 2 ; -6). Viết phương trình mặt cầu (S) tiếp xúc với hai đường thẳng AC và BD lần lượt tại A và B.
DANH SÁCH CÂU HỎI
-
[Trong không gian với hê tọa độ Oxyz, cho các điểm A (3 ; -1 ; 1), B (-1 - Luyện Tập 365]
-
[Trong không gian với hệ tọa độ Oxyz, viết phương trình mặt cầu (S) có tâ - Luyện Tập 365]
-
[Trong không gian với hệ tọa độ Oxyz,cho điểm M(3;-1;1), mặt phẳng (P) : - Luyện Tập 365]
-
[Trong không gian với hệ tọa độ Oxy cho hai mặt phẳng (P): x– 2y + - Luyện Tập 365]
-
[Trong không gian với hệ tọa độ Oxyz, cho (P) ; 2x + y -z =0, d: - Luyện Tập 365]
-
[Trong không gian với hệ tọa độ Oxyz, cho (P) : 2x + y -z =0, d: - Luyện Tập 365]
-
[Trong không gian với hệ tọa độ Oxyz, cho tam giác ABC có B(1;4;3), phươn - Luyện Tập 365]
-
[Trong không gian với hệ tọa độ Oxyz, cho điểm H(2;-1;1) và đường thằng&n - Luyện Tập 365]
-
[Trong không gian với hệ tọa độ Oxyz,cho đường thẳng d: - Luyện Tập 365]
-
[Trong không gian với hệ trục tọa độ Oxyz, cho các điểm A (1 ; 0; 0), B ( - Luyện Tập 365]
-
[Trong không gian với hệ tọa độ Oxyz, cho hai đường thẳng: d: - Luyện Tập 365]
-
[Trong không gian với hệ tọa độ Oxyz, cho d: - Luyện Tập 365]
-
[Trong không gian với hệ tọa độ Oxyz, cho: (P): x - 2y + 2z + 1 = 0 cắt m - Luyện Tập 365]
-
[Trong không gian với hệ trục tọa độ vuông góc Oxyz, cho hai mặt phẳng (P - Luyện Tập 365]
-
[Trong không gian cho mặt phẳng Oxyz, cho mặt phẳng (P): x + 2y - 2z + 1 - Luyện Tập 365]
= 
= 
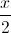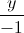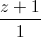, biết rằng mặt cầu (S) đi qua A (2 ; -1 ; 0) và cắt (Oxy) theo giao tuyến là đường tròn có bán kính là √5.
= 
= 
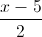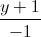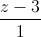. Tìm điểm đối A ∈ (P) sao cho AM ⊥ ∆ và khoảng cách từ A đến đường thẳng ∆ bằng √66
= 
= 
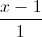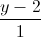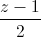. Viết phương trình mặt phẳng (R) chứa giao tuyến của hai mặt phẳng (P) và (Q), đồng thời song song với d.
= 
= 
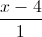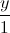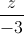và M (1;-1;1). Viết phương trình đường thẳng ∆ đi qua M, vuông góc với đường thẳng d và tạo với (P) một góc bằng 300 .
= 
= 
, ∆: 
= 
= 
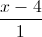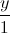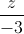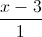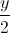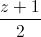. Tìm tọa độ điểm M nằm trên (P), điểm N trên đường thẳng d sao cho M và N đối xứng với nhau qua đường thẳng ∆.
= 
= 
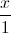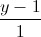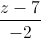, CH: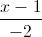 
=
=
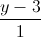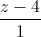Tìm tọa độ các đỉnh A và C
= 
= 
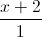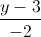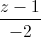. Xét hình bình hành ABCD có A(1; 0; 0), C(2; 2; 2), D ∈ d. Tìm tọa độ đỉnh B biết diện tích của hình bình hành ABCD bằng 3√2.
= 
= 
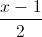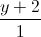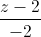, d' : 
= 
= 
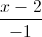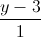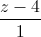và (α): x - y + z - 6 = 0. Tìm điểm M nằm trên đường thẳng d' sao cho đường thẳng đi qua M và song song với đường thẳng d cắt mặt phẳng (α) tại điểm N sao cho MN = 3
= 
= 
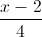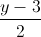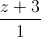, (P): -x + y + 2z + 5 = 0. Viết phương trình đường thẳng ∆ nằm trong (P) song song với đường thẳng d và cách đường thẳng d một khoảng bằng √14.