Câu Hỏi Luyện Tập Hình Giải Tích Trong Không Gian - Page 25 of 28 - Luyện Tập 365

/ Câu hỏi luyện tập / Luyện Thi Đại Học Môn Toán / Hình Giải Tích Trong Không Gian

DANH SÁCH CÂU HỎI

[Trong không gian với hệ tọa độ Oxyz, cho điểm A(-1;1;3), đường thẳng d - Luyện Tập 365]

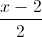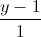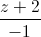Trong không gian với hệ tọa độ Oxyz, cho điểm A(-1;1;3), đường thẳng d₁: $\frac{x-2}{2}$ = $\frac{y-1}{1}$ = $\frac{z+2}{-1}$ và mặt phẳng (P): x+2y+Z-3=0. Viết phương trình đường thẳng d₂ đi qua điểm A biết rằng d₂ cắt d₁và tạo với mặt phẳng (P) một góc 30^o.

Chi tiết
[Trong không gian tọa độ Oxyz cho mặt phẳng (P): x - 2y -2z + 2 = 0 và đi - Luyện Tập 365]

Trong không gian tọa độ Oxyz cho mặt phẳng (P): x - 2y -2z + 2 = 0 và điểm A(0 ; 0 ; 1). Viết phương trình mặt cầu tiếp xúc với mặt phẳng (P) tại A và tiếp xúc với mặt phẳng (xOy).

Chi tiết
[Trong không gian Oxyz cho các điểm A(3 ; 0 ; 2), B(1 ; 2 ; 1) và đường t - Luyện Tập 365]

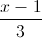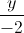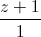Trong không gian Oxyz cho các điểm A(3 ; 0 ; 2), B(1 ; 2 ; 1) và đường thẳng d có phương trình: $\frac{x-1}{3}$ = $\frac{y}{-2}$ = $\frac{z+1}{1}$ . Gọi A₁ và B₁ lần lượt là hình chiếu của A và B trên đường thẳng d. Tìm tọa độ điểm A₁ , B₁.

Chi tiết
[Trong không gian Oxyz cho mặt phẳng (P): x - 2y + 2z - 1 = 0 và hai đườn - Luyện Tập 365]

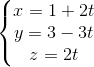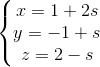Trong không gian Oxyz cho mặt phẳng (P): x - 2y + 2z - 1 = 0 và hai đường thẳng d₁ và d₂ lần lượt có phương trình: d₁ : $\left\{\begin{matrix} x=1+2t & \\y=3-3t & \\z=2t & \end{matrix}\right.$ d₂ : $\left\{\begin{matrix} x=1+2s & \\y=-1+s & \\ z=2-s & \end{matrix}\right.$ , s và t là tham số. Lập phương trình mặt phẳng (Q) chứa d₁ và vuông góc với mặt phẳng (P)

Chi tiết
[Trong không gian Oxyz cho đường thẳng d: - Luyện Tập 365]

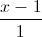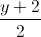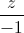Trong không gian Oxyz cho đường thẳng d: $\frac{x-1}{1}$ = $\frac{y+2}{2}$ = $\frac{z}{-1}$ và điểm A(1; 2; 3). Viết phương trình đường thẳng (∆ ) đi qua A, vuông góc với d vá cách d một khoảng rất lớn.

Chi tiết
[Trong không gian Oxyz cho mặt phẳng (P): x - 2y + 2z - 1 = 0 và hai đườn - Luyện Tập 365]

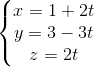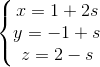Trong không gian Oxyz cho mặt phẳng (P): x - 2y + 2z - 1 = 0 và hai đường thẳng d₁ và d₂ lần lượt có phương trình: d₁ : $\left\{\begin{matrix} x=1+2t & \\y=3-3t & \\z=2t & \end{matrix}\right.$ d₂ : $\left\{\begin{matrix} x=1+2s & \\y=-1+s & \\ z=2-s & \end{matrix}\right.$ , s và t là tham số. Tìm các điểm M ∈ d₁ ; N ∈ d₂ sao cho MN song song với (P) và cách (P) một khoảng bằng 2

Chi tiết
[Trong không gian với hệ tọa độ Oxyz, cho các điểm A(3 ; 1 ; 1), B(0 ; 1 - Luyện Tập 365]

Trong không gian với hệ tọa độ Oxyz, cho các điểm A(3 ; 1 ; 1), B(0 ; 1 ; 4), C(-1 ; -3 ; 1) và mặt phẳng (α): x + y - 2z + 4 = 0. Viết phương trình mặt cầu (S) có tâm nằm trên mặt phẳng (α) và đi qua ba điểm A, B, C.

Chi tiết
[Trong không gian với hệ tọa độ Oxyz, cho hai mặt phẳng (α): 2x + 2y + z - Luyện Tập 365]

Trong không gian với hệ tọa độ Oxyz, cho hai mặt phẳng (α): 2x + 2y + z + 5 = 0, (β): 4x - 3z + 23 = 0. Viết phương trình mặt cầu (S) tiếp xúc với (β) tại A(5;2;1) và cắt (α) theo một đường tròn có diện tích bằng 16π. Biết rằng tâm của mặt cầu (S) có tọa độ nguyên.

Chi tiết
[Trong không gian với hệ tọa độ Oxyz, cho A(1 ; -1 ; 1), mặt phẳng (P): 2 - Luyện Tập 365]

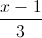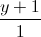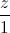Trong không gian với hệ tọa độ Oxyz, cho A(1 ; -1 ; 1), mặt phẳng (P): 2x + y - 2z + 2 = 0, đường thẳng d: $\frac{x-1}{3}$ = $\frac{y+1}{1}$ = $\frac{z}{1}$ . Lập phương trình mặt cầu (S) có tâm nằm trên đường thẳng d, có bán kính nhỏ nhất, tiếp xúc với mặt phẳng (P) và đi qua điểm A

Chi tiết
[Trong không gian Oxyz, cho mặt phẳng (P): x + 2y – 2z + 1 = 0 và - Luyện Tập 365]

Trong không gian Oxyz, cho mặt phẳng (P): x + 2y – 2z + 1 = 0 và hai điểm A(1; 7;-1), B(4; 2; 0). Lập phương trình đường thẳng d là hình chiếu vuông góc của đường thẳng AB trên mặt phẳng (P).

Chi tiết
[Trong không gian với hệ tọa độ Oxyz, cho 2 mặt phẳng (α): x - 2y + 2z - - Luyện Tập 365]

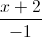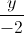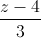Trong không gian với hệ tọa độ Oxyz, cho 2 mặt phẳng (α): x - 2y + 2z - 3 = 0, (β): 2x + y - 2z - 4 = 0 và đường thẳng d: $\frac{x+2}{-1}$ = $\frac{y}{-2}$ = $\frac{z-4}{3}$ . Viết phương trình mặt cầu (S) có tâm I nằm trên đường thẳng d và tiếp xúc với hai mặt phẳng (α) và (β)

Chi tiết
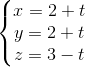[Trong không gian Oxyz cho hai đường thẳng d1,d2 lầ - Luyện Tập 365]

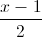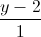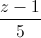Trong không gian Oxyz cho hai đường thẳng d₁,d₂ lần lượt có phương trình: d₁: $\left\{\begin{matrix} x=2+t\\y=2+t \\z=3-t \end{matrix}\right.$ d₂: $\frac{x-1}{2}$ = $\frac{y-2}{1}$ = $\frac{z-1}{5}$ . Viết phương trình mặt phẳng cách đều hai đường thẳng d₁,d₂

Chi tiết
[Trong không gian với hệ tọa độ Oxyz, cho điểm M(1 ; 2 ; -1), mặt phẳng ( - Luyện Tập 365]

Trong không gian với hệ tọa độ Oxyz, cho điểm M(1 ; 2 ; -1), mặt phẳng (α): x + y + z = 0. Viết phương trình mặt phẳng (P) đi qua O, vuông góc với (α) và cách điểm M một khoảng bằng √2

Chi tiết
[Cho mặt phẳng (P) có phương trình: x-2y+2z-1=0 và các đường thẳng - Luyện Tập 365]

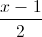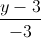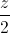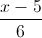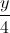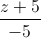Cho mặt phẳng (P) có phương trình: x-2y+2z-1=0 và các đường thẳng d₁: $\frac{x-1}{2}$ = $\frac{y-3}{-3}$ = $\frac{z}{2}$ ; d₂: $\frac{x-5}{6}$ = $\frac{y}{4}$ = $\frac{z+5}{-5}$ . Tìm các điểm M,N lần lượt thuộc d₁,d₂ sao cho MN// (P) và cách (P) một khoảng bằng 2.

Chi tiết
[Trong không gian với hệ tọa độ Oxyz, cho đường thẳng∆ có phương tr - Luyện Tập 365]

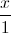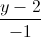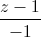Trong không gian với hệ tọa độ Oxyz, cho đường thẳng ∆ có phương trình ∆: $\frac{x}{1}$ = $\frac{y-2}{-1}$ = $\frac{z-1}{-1}$ . Viết phương trình mặt phẳng (P) chưa đường thẳng ∆, biết rằng (P) tạo với các trục Oy, Oz những góc bằng nhau.

Chi tiết