DANH SÁCH CÂU HỎI

• [Trong không gian với hệ tọa độ Oxyz, cho hai đường thẳng: D1: - Luyện Tập 365]

  Trong không gian với hệ tọa độ Oxyz, cho hai đường thẳng: D₁: 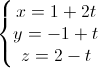Và D₂ là giao tuyến của hai mặt phẳng (P) : 3y – z – 7 = 0, (Q): 3x + 3y – 2z -17 = 0. Cho A, B chạy trên D₁; C, D chạy trên D₂ sao cho AB = 5cm, CD = 7cm. Tính thể tích của tứ diện ABCD.  

  Chi tiết
• [Trong không gian với hệ trục tọa độ Đêcac vuông góc Oxyz cho 3 điểm A(3 - Luyện Tập 365]

  Trong không gian với hệ trục tọa độ Đêcac vuông góc Oxyz cho 3 điểm A(3 ; 0 ; 0) , B(0 ; 3 ; 0) , C(0 ; 0 ; 3) và H là hình chiếu của O lên (ABC). Gọi D là điểm đối xứng với H qua O. Lập phương trình mặt cầu ngoại tiếp hình chóp ABCD.

  Chi tiết
• [Cho hai đường thẳng: d1: - Luyện Tập 365]

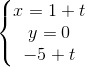  Cho hai đường thẳng:   d₁:   và d₂:  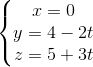. Chứng minh  d₁ và d₂ chéo nhau.

  Chi tiết
• [Cho hai đường thẳng: d1: - Luyện Tập 365]

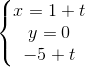  Cho hai đường thẳng:   d₁:   và d₂:  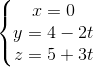. Viết phương trình chính tắc của đường vuông góc chung của d₁ và d_2.

  Chi tiết
• [Cho hình lăng trụ đứng tam giác ABC.A'B'C' có đáy ABC là tam giác vuông - Luyện Tập 365]

  Cho hình lăng trụ đứng tam giác ABC.A'B'C' có đáy ABC là tam giác vuông cân tại A, cạnh AB = a, cạnh AA' = 2a. Tính khoảng cách giữa hai đường thẳng chéo nhau A'B và B'C.

  Chi tiết
• [Trong không gian với trục tọa độ Oxyz, cho hai mặt phẳng - Luyện Tập 365]

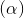  Trong không gian với trục tọa độ Oxyz, cho hai mặt phẳng :  x + y - 3z - 2 = 0 và (P): x + 2y - z - 4 = 0. Viết phương trình đường thẳng ∆  đi qua điểm M(1; 0; -2) song song với mặt phẳng  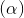đồng thời tạo với mặt phẳng (P) một góc  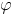= 30°.

  Chi tiết
• [Cho đường thẳng d: - Luyện Tập 365]

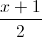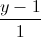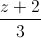  Cho đường thẳng d: == và mặt phẳng (P): x+y+z+8=0. Gọi A là giao điểm của d với mặt phẳng (P). Viết phương trình đường thẳng ∆ qua A vuông góc với d và năm trong mặt phẳng (P).

  Chi tiết
• [Viết phương trình đường thẳng đi qua A(-1;1;2) song song với mặt phẳng ( - Luyện Tập 365]

  Viết phương trình đường thẳng đi qua A(-1;1;2) song song với mặt phẳng (P):x-y-z+5=0 đồng thời vuông góc với đường thẳng: ==

  Chi tiết
• [Trong không gian với hệ trục tọa độ vuông góc Oxyz, cho mặt phẳng (P) có - Luyện Tập 365]

  Trong không gian với hệ trục tọa độ vuông góc Oxyz, cho mặt phẳng (P) có phương trình: 2x – y – 2z – 12 = 0 và hai điểm A(2; 1; 4), B(1; 1; 3). Tìm tập hợp tất cả các điểm M trên (P) sao cho diện tích của tam giác  MAB có giá trị nhỏ nhất.  

  Chi tiết
• [Trong không gian với hệ tọa độ Oxyz cho A(2;0;0), M(1;1;1). Giả sử (P) l - Luyện Tập 365]

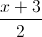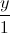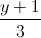
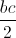  Trong không gian với hệ tọa độ Oxyz cho A(2;0;0), M(1;1;1). Giả sử (P) là mặt phẳng thay đổi nhưng luôn qua đường thẳng đường thằng AM và cắt các trục Oy,Oz lần lượt tại B(0;b;0), C(0;0;c) với b,c>0 Chứng minh: b+c= và tìm b,c để S_∆ABC nhỏ nhất

  Chi tiết
• [Trong không gian Oxyz cho đường thẳng d có phương trình: - Luyện Tập 365]

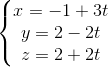  Trong không gian Oxyz cho đường thẳng d có phương trình:  và cho điểm A(1;2;-1); B(7;-2;3)  Tìm điểm I thuộc đường thẳng d sao cho: IA+IB nhỏ nhất

  Chi tiết
• [Trong không gian với hệ tọa độ Oxyz cho A(1;0;0); B(2;0;2); C(0;0;3). tì - Luyện Tập 365]

  Trong không gian với hệ tọa độ Oxyz cho A(1;0;0); B(2;0;2); C(0;0;3). tìm tọa độ trực tâm của ∆ABC.

  Chi tiết
• [Trong không gian Oxyz cho điểm A(4;2;2), B(0;0;7) và đường thẳng d - Luyện Tập 365]

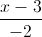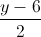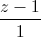  Trong không gian Oxyz cho điểm A(4;2;2), B(0;0;7)  và đường thẳng d có phương trình: ==. Chứng minh hai đường thẳng AB và d cùng thuộc một mặt phẳng. Tìm C ∈ (d) sao cho ∆ABC cân ở A.

  Chi tiết
• [Trong không gian với hệ tọa độ Oxyz, viết phương trình mặt phẳng (α) đi - Luyện Tập 365]

  Trong không gian với hệ tọa độ Oxyz, viết phương trình mặt phẳng (α) đi qua điểm I(1;-2;3) biết (α) vuông góc với mặt phẳng (β): x+2y-z+2010=0 và tạo với mặt phẳng (Oxy) một góc 45^o.

  Chi tiết
• [Trong không gian Oxyz cho các điểm A(3 ; 0 ; 2), B(1 ; 2 ; 1) và đường t - Luyện Tập 365]

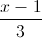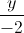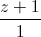  Trong không gian Oxyz cho các điểm A(3 ; 0 ; 2), B(1 ; 2 ; 1) và đường thẳng d có phương trình:  =  =  Tìm điểm M thuộc đường thẳng d sao cho  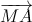+  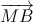có độ dài nhỏ nhất

  Chi tiết