Trong không gian với hệ tọa độ vuông góc với Oxyz, cho hình chóp tứ giác đẻ S.ABCD, biết S(3; 2; 4); A(1; 2; 3); C(3; 0; 3). Xác định tọa độ tâm I của mặt cầu ngoại tiếp hình chóp S.ABCD.
DANH SÁCH CÂU HỎI
-
[Trong không gian với hệ tọa độ vuông góc với Oxyz, cho hình chóp tứ giác - Luyện Tập 365]
-
[Trong không gian với hệ tọa độ vuông góc với Oxyz, cho hình chóp tứ giác - Luyện Tập 365]
-
[Trong không gian Oxyz hãy lập phương trình mặt phẳng (P) chứa trục Oz và - Luyện Tập 365]
-
[Trong không gian Oxyz cho A(3;0;0), B( 0 ;0; 1). Lập phương trình mặt ph - Luyện Tập 365]
-
[Trong không gian với hệ tọa độ Đề - các vuông góc Oxyz cho A( 3;0;0), B( - Luyện Tập 365]
-
[Trong không gian Oxyz cho hai điểm A(2;2;3), B(5;0;2) và đường thẳng d : - Luyện Tập 365]
-
[Cho hình lập phương ABCD.A’B’C’D’ có cạnh bằng 1. Đặt hệ tọa độ Oxyz sao - Luyện Tập 365]
-
[Trong không gian cho Oxyz cho lăng trụ đứng OAB.O1A1 - Luyện Tập 365]
-
[Trong không gian với hệ trục tọa độ Đê-các vuông góc với Oxyz cho - Luyện Tập 365]
-
[Trong không gian với hệ trục tọa độ Đê-các vuông góc với Oxyz cho - Luyện Tập 365]
-
[Trong không gian Oxyz cho A(3; 1; 1) B(7; 3; 9) C(2; 2; 2) và mặt phẳng - Luyện Tập 365]
-
[Cho M(1; 2; 1).Viết phương trình mặt phẳng (P) đi qua M cắt các tia Ox, - Luyện Tập 365]
-
[Trong hệ tọa độ Oxyz cho điểm A(10 ; 3 ; -1), đường thẳng d có phương tr - Luyện Tập 365]
-
[Lập phương trình mặt phẳng (P) chứa đường thẳng (d): - Luyện Tập 365]
-
[Trong không gian với hệ tọa độ Đề các vuông góc Oxyz cho họ đường - Luyện Tập 365]
= 
= 
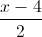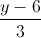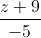a)Chứng minh rằng đường thẳng d và đường thẳng qua A và B chéo nhau. Viết phương trình đường vuông góc chung của hai đường thẳng ấy. b)Xác định điểm M trên d sao cho diện tích tam giác MAB đạt giá trị nhỏ nhất. phương trình đường thẳng đi qua A và B có VTCP = (3;-2;-1).
= 
= 
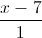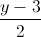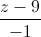: l: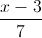 
= 
= 
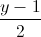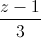(P): x + y + z + 3 = 0. Tìm M để |
+ 
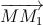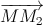| đạt giá trị nhỏ nhất biết M1(3; 1; 1); M2(7; 3; 9)
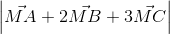nhỏ nhất.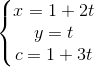
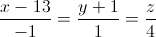và tiếp xúc với mặt cầu (S): x2 + y2 + z2 – 2x – 4y – 6z – 67 = 0
= 
= 
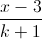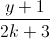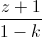, trong đó k là tham số ( k ≠ ± 1; 
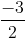). Chứng minh rằng họ đường thẳng dk luôn luôn nằm trong một mặt phẳng cố định. Viết phương trình mặt phẳng đó.