Trong không gian với hệ tọa độ Oxyz cho 2 điểm A(1 ; -1 ; 2) và B(3 ; 1 ; 0) và mặt phẳng (P) có phương trình: x - 2y - 4z + 8 = 0. Tìm tọa độ điểm C nằm trong mặt phẳng (P) sao cho CA = CB và mặt phẳng (ABC) vuông góc với mặt phẳng (P).
DANH SÁCH CÂU HỎI
-
[Trong không gian với hệ tọa độ Oxyz cho 2 điểm A(1 ; -1 ; 2) và B(3 ; 1 - Luyện Tập 365]
-
[Trong không gian với hệ tọa độ Oxyz cho 2 điểm A(1 ; -1 ; 2) và B(3 ; 1 - Luyện Tập 365]
-
[Trong không gian Oxyz, cho đường thẳng ∆1 : - Luyện Tập 365]
-
[Trong oxyz cho mặt cầu (S): x2 + y2 + z - Luyện Tập 365]
-
[Cho 3 điểm A(1, 2, -1); B(2, 1, 1); C(0, 1, 2) và đường thẳng d:&n - Luyện Tập 365]
-
[Trong không gian với hệ tọa độ Đề-các vuông góc với Oxyz cho 4 đường thẳ - Luyện Tập 365]
-
[Trong không gian Oxyz, cho mặt phẳng (P): x+3y- - Luyện Tập 365]
-
[Trong không gian với hệ tọa độ vuông góc với Oxyz cho đường thẳng d là g - Luyện Tập 365]
-
[Trong không gian với hệ tọa độ vuông góc Oxyz cho các điểm: A(2 ; 0 ; 0) - Luyện Tập 365]
-
[Trong không gian Oxyz cho 3 đường thẳng: - Luyện Tập 365]
-
[Trong không gian với hệ trục tọa độ vuông góc Oxyz cho 3 điểm A(-1; 3; - - Luyện Tập 365]
-
[Trong không gian Oxyz cho mặt cầu (S): x2+y2+z - Luyện Tập 365]
-
[Cho tứ diện S.ABC có đáy ABC là tam giác vuông tại B, SA ⊥ (ABC). AB = a - Luyện Tập 365]
-
[Trong không gian Oxyz cho mặt cầu (S): x2+y2+z - Luyện Tập 365]

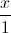 =
= 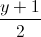 =
= 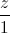 Và ∆2:
Và ∆2: 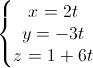 . Viết phương trình đường thẳng d cắt ∆1, ∆2 và song song với ∆3 là giao tuyến của hai mặt phẳng (P) : 4x – y – 9 = 0 và (Q) : y + 2z – 13 = 0.
. Viết phương trình đường thẳng d cắt ∆1, ∆2 và song song với ∆3 là giao tuyến của hai mặt phẳng (P) : 4x – y – 9 = 0 và (Q) : y + 2z – 13 = 0.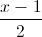 =
= 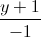 =
= 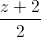 . Viết phương trình đường thẳng đi qua trực tâm tam giác ABC nằm trong (ABC) và vuông góc với d
. Viết phương trình đường thẳng đi qua trực tâm tam giác ABC nằm trong (ABC) và vuông góc với d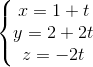 ; d2:
; d2: 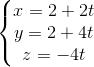 ; d3:
; d3: 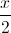 =
= 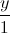 =
= 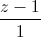 ; d4:
; d4: 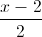 =
= 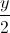 =
= 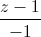 Chứng minh d1, d2 cùng thuộc mặt phẳng (α). Viết phương trình mặt phẳng (α) và chứng minh có một đường thẳng cắt cả 4 đường thẳng trên. Viết phương trình đường thẳng đó
Chứng minh d1, d2 cùng thuộc mặt phẳng (α). Viết phương trình mặt phẳng (α) và chứng minh có một đường thẳng cắt cả 4 đường thẳng trên. Viết phương trình đường thẳng đó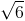 z-21=0 và mặt cầu (S) có bán kính bằng 5, tâm thuộc tia Ox và tiếp xúc với mặt phẳng Oxy. Tính bán kính và tọa độ tâm của đường tròn (C) là giao của mặt cầu (S) với mặt phẳng (P).
z-21=0 và mặt cầu (S) có bán kính bằng 5, tâm thuộc tia Ox và tiếp xúc với mặt phẳng Oxy. Tính bán kính và tọa độ tâm của đường tròn (C) là giao của mặt cầu (S) với mặt phẳng (P).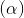 : x - y - 1 = 0 và mặt phẳng
: x - y - 1 = 0 và mặt phẳng 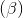 : y - z + 6 = 0. Hãy lập phương trình mặt phẳng (P) chứa d và tạo với mặt phẳng Oyz góc 45°.
: y - z + 6 = 0. Hãy lập phương trình mặt phẳng (P) chứa d và tạo với mặt phẳng Oyz góc 45°. 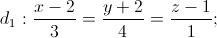
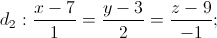
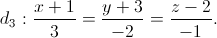 Lập phương trình đường thẳng ∆ cắt d1; d2 và song song với d3.
Lập phương trình đường thẳng ∆ cắt d1; d2 và song song với d3.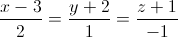 và mặt phẳng (P) có phương trình: x+ y+ z +2=0. VIết phương trình đường thẳng ∆ thỏa mãn ∆ ⊥ d, (∆)⊂(P) và d(M, ∆) = √42 (M là giao điểm của d và P).
và mặt phẳng (P) có phương trình: x+ y+ z +2=0. VIết phương trình đường thẳng ∆ thỏa mãn ∆ ⊥ d, (∆)⊂(P) và d(M, ∆) = √42 (M là giao điểm của d và P).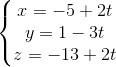 và d2:
và d2: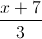 =
=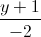 =
=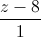 Viết phương trình mặt phẳng (P) tiếp xúc với mặt cầu (S) và song song với hai đường thẳng d1,d2.
Viết phương trình mặt phẳng (P) tiếp xúc với mặt cầu (S) và song song với hai đường thẳng d1,d2.