Câu Hỏi Luyện Tập Hình Giải Tích Trong Không Gian - Page 21 of 28 - Luyện Tập 365

/ Câu hỏi luyện tập / Luyện Thi Đại Học Môn Toán / Hình Giải Tích Trong Không Gian

DANH SÁCH CÂU HỎI

[Trong không gian với hệ trục tọa độ Oxyz, cho đường thẳng ∆: - Luyện Tập 365]

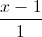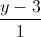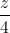Trong không gian với hệ trục tọa độ Oxyz, cho đường thẳng ∆: $\frac{x-1}{1}$ = $\frac{y-3}{1}$ = $\frac{z}{4}$ và điểm M(0; -2; 0). Viết phương trình mặt phẳng (P) đi qua điểm M song song với đường thẳng ∆ đồng thời khoảng cách giữa đường thẳng ∆ và mặt phẳng (P) bằng 4.

Chi tiết
[Trong không gian với hệ trục tọa độ Oxyz, cho hai đường thẳng d1 - Luyện Tập 365]

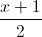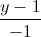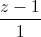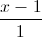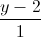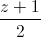Trong không gian với hệ trục tọa độ Oxyz, cho hai đường thẳng d₁ : $\frac{x+1}{2}$ = $\frac{y-1}{-1}$ = $\frac{z-1}{1}$ ; d₂ : $\frac{x-1}{1}$ = $\frac{y-2}{1}$ = $\frac{z+1}{2}$ và mặt phẳng (P) : x – y – 2z + 3 = 0. Viết phương trình chính tắc của đường thẳng ∆, biết ∆ nằm trên mặt phẳng ( P ) và ∆ cắt hai đường thẳng d₁, d₂.

Chi tiết
[Trong không gian với hệ trục Oxyz cho điểm A(1;0;1), B(2;1;2) và mặt phẳ - Luyện Tập 365]

Trong không gian với hệ trục Oxyz cho điểm A(1;0;1), B(2;1;2) và mặt phẳng (Q):x+2y+3z+3=0. Lập phương trình mặt phẳng (P) đi qua A,B và vuông góc với (Q)

Chi tiết
[Trong không gian với hệ trục tọa độ Oxyz cho bốn điểm A(1; -1;2), B(1;3; - Luyện Tập 365]

Trong không gian với hệ trục tọa độ Oxyz cho bốn điểm A(1; -1;2), B(1;3;2), C(4;3;2), D(4;-1;2) và mặt phẳng (P) có phương trình: x + y + z – 2 = 0. Gọi A’ là hình chiếu của A lên mặt phẳng Oxy. Gọi (S ) là mặt cầu đi qua bốn điểm A’, B, C, D. Xác định tọa độ tâm và tính bán kính đường tròn (K) là giao của (P) và (S).

Chi tiết
[Trong không gian với hệ trục tọa độ Oxyz cho (P): x + 2y – z + 5 = 0 và - Luyện Tập 365]

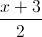Trong không gian với hệ trục tọa độ Oxyz cho (P): x + 2y – z + 5 = 0 và đường thẳng (d): $\frac{x+3}{2}$ = y + 1 = z – 3, điểm A(-2;3;4). Gọi ∆ là đường thẳng nằm trên (P) đi qua giao điểm của (d) và (P) đồng thời vuông góc với d. Tìm trên ∆ điểm M sao cho khoảng cách AM ngắn nhất.

Chi tiết
[Trong không gian với hệ tọa độ Oxyz, cho điểm A(√2; - 5; 0). Viết phương - Luyện Tập 365]

Trong không gian với hệ tọa độ Oxyz, cho điểm A(√2; - 5; 0). Viết phương trình đường thẳng d qua A biết d cắt Oz và tạo với Oz một góc 60⁰.

Chi tiết
[Trong không gian với hệ tọa độ Oxyz cho hai điểm A(1;4;2), B(-1;2;4) và - Luyện Tập 365]

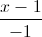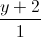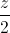Trong không gian với hệ tọa độ Oxyz cho hai điểm A(1;4;2), B(-1;2;4) và đường thẳng (d): $\frac{x-1}{-1}$ = $\frac{y+2}{1}$ = $\frac{z}{2}$ . Tìm tọa độ điểm M trên đường thẳng (d) sao cho P=MA²+MB² nhỏ nhất

Chi tiết
[Trong không gian Oxyz, cho điểm A(5; 5 ; 0) và đường thẳng d: - Luyện Tập 365]

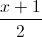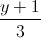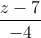Trong không gian Oxyz, cho điểm A(5; 5 ; 0) và đường thẳng d: $\frac{x+1}{2}$ = $\frac{y+1}{3}$ = $\frac{z-7}{-4}$ . Tìm tọa độ các điểm B, C thuộc d sao cho tam giác ABC vuông cân tại A và BC = 2√17.

Chi tiết
[Trong không gian với hệ tọa độ Oxyz, cho hai điểm A(1;2;-1), B(2 - √2; 2 - Luyện Tập 365]

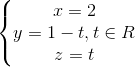Trong không gian với hệ tọa độ Oxyz, cho hai điểm A(1;2;-1), B(2 - √2; 2-; -3) và đường thẳng d: $\left\{\begin{matrix}x=2\\y=1-t,t\in R\\z=t\end{matrix}\right.$ , t ∈ R .Tìm điểm C trên đường thẳng d sao cho chu vi tam giác ABC nhỏ nhất.

Chi tiết
[Trong không gian với hệ tọa độ Oxyz, cho hình vuông ABCD có đỉnh A(1; 2; - Luyện Tập 365]

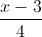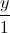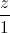Trong không gian với hệ tọa độ Oxyz, cho hình vuông ABCD có đỉnh A(1; 2; 1) và đường chéo BD có phương trình: $\frac{x-3}{4}$ = - $\frac{y}{1}$ = $\frac{z}{1}$ .Tìm tọa độ các đỉnh còn lại của hình vuông.

Chi tiết
[Cho A(1;0;-2) và B(3;1;0) và đường thẳng d: - Luyện Tập 365]

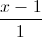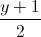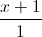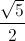Cho A(1;0;-2) và B(3;1;0) và đường thẳng d: $\frac{x-1}{1}$ = $\frac{y+1}{2}$ = $\frac{x+1}{1}$ .Tìm tọa độ điểm M thuộc d saoc cho diện tích tam giác ABM bằng $\frac{\sqrt{5}}{2}$ .

Chi tiết
[Trong không gian tọa độ Oxyz cho hình lăng trụ đứng tam giác ABC.A’B’C’ - Luyện Tập 365]

Trong không gian tọa độ Oxyz cho hình lăng trụ đứng tam giác ABC.A’B’C’ với A(0;-3;0), B(4;0;0), C(0;3;0), B’(4;0;4). Gọi M là trung điểm của A’B’. Mặt phẳng (P) đi qua hai điểm A,M và song song với BC’, (P) cắt A’C’ tại N. Tính độ dài MN

Chi tiết
[Trong không gian Oxyz, cho tam giác ABC với điểm M(1;0;2) thuộc cạ - Luyện Tập 365]

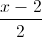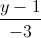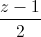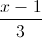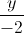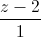Trong không gian Oxyz, cho tam giác ABC với điểm M(1;0;2) thuộc cạnh BC, đường phân giác trong góc B và đường cao kẻ từ đỉnh A lần lượt có phương trình: d₁: $\frac{x-2}{2}$ = $\frac{y-1}{-3}$ = $\frac{z-1}{2}$ ; d₂ : $\frac{x-1}{3}$ = $\frac{y}{-2}$ = $\frac{z-2}{1}$ Tính khoảng cách từ điểm M đến đường thẳng AB.

Chi tiết
[Trong không gian Oxyz, cho bốn điểm A(2;2;-1), B(1;4;-1), C(2;4;3), D(2; - Luyện Tập 365]

Trong không gian Oxyz, cho bốn điểm A(2;2;-1), B(1;4;-1), C(2;4;3), D(2;4;-1). Viết phương trình mặt phẳng (α) tiếp xúc với mặt cầu ngoại tiếp tứ diện ABCD và song song với mặt phẳng (BCD).

Chi tiết
[Trong không gian Oxyz, cho mặt phẳng (α ): 3x + 2y – z + 4 = 0 và điểm M - Luyện Tập 365]

Trong không gian Oxyz, cho mặt phẳng (α ): 3x + 2y – z + 4 = 0 và điểm M(2;2;0). Xác định tọa độ điểm N sao cho MN vuông góc với (α ) đồng thời N cách đều gốc tọa độ O và mặt phẳng (α ).

Chi tiết