Trong không gian với hệ tọa độ Oxyz, cho A(0 ; 0; 3), M(1; 2; 0). Viết phương trình mặt phẳng (P) qua A và cắt Ox, Oy lần lượt tại B, C sao cho ∆ABC có trọng tâm thuộc AM.
DANH SÁCH CÂU HỎI
-
[Trong không gian với hệ tọa độ Oxyz, cho A(0 ; 0; 3), M(1; 2; 0). Viết p - Luyện Tập 365]
-
[Trong không gian với hệ toạ độ Oxyz, cho - Luyện Tập 365]
-
[Trong không gian với hệ toạ độOxyz, cho mặt phẳng (P ) - Luyện Tập 365]
-
[Trong không gian với hệ Oxyz, cho đường thẳng∆: - Luyện Tập 365]
-
[Trong không gian với hệ tọa độ Oxyz, cho các điểm A(-1;3 ; -2) và mặt ph - Luyện Tập 365]
-
[Trong không gian với hệ tọa độ Oxyz, cho điểm A(3; 5; 0) và mặt phẳng (P - Luyện Tập 365]
-
[Trong không gian với hệ tọa độ Oxyz, cho các điểm A(1; -1;1), B(-1;2;3) - Luyện Tập 365]
-
[Trong không gian với hệ tọa độ Oxyz, cho các điểm A(-1; -1;-2), B(0;1;1) - Luyện Tập 365]
-
[Trong không gian với hệ tọa Oxyz, cho đường thẳng ∆: - Luyện Tập 365]
-
[Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng (P): 2x + 3y + z – 11 - Luyện Tập 365]
-
[Trong không gian với hệ tọa độ Oxyz, cho điểm A(4; -1;3) và đường thẳng - Luyện Tập 365]
-
[Trong không gian với hệ tọa độ Oxyz, cho điểm A(-1; 3;2) và mặt phẳng (P - Luyện Tập 365]
-
[Trong không gian hệ tọa độ Oxyz, cho đường thẳng∆: - Luyện Tập 365]
-
[Trong không gian Oxyz, cho mặt cầu (S) và mặt phẳng (P) có phương trình: - Luyện Tập 365]
-
[Trong không gian Oxyz, cho điểm A(1; – 2; 3) và đường thẳng d có phương - Luyện Tập 365]
với A(-1;1;-3), B(3;1;1), C(3;-3;-1). Tìm toạ độ điểm M sao cho các đường thẳng MA, MB, và MC đôi một vuông góc với nhau.
= 
= 
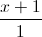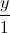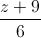, ∆2: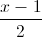 
= 
= 
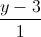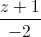. Xác định tọa độ điểm M thuộc đường thẳng ∆1 sao cho khoảng cách từ M đến đường thẳng ∆2 và khoảng cách từ M đến mặt phẳng (P) bằng nhau
= 
= 
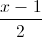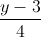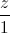và mặt phẳng (P): 2x - y + 2z = 0. Viết phương trình mặt cầu có tâm thuộc đường thẳng ∆, bán kính bằng 1 và tiếp xúc với mặt phẳng (P)
= 
= 
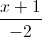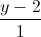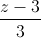. Viết phương trình đường thẳng đi qua A, vuông góc với hai đường thẳng AB và ∆.
= 
= 
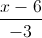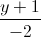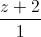và điểm A(1;7;3). Viết phương trình mặt phẳng (P) đi qua A và vuông góc với ∆. Tìm tọa độ điểm M thuộc ∆ sao cho AM = 2√30.
= 
= 
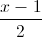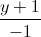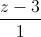. Tìm tọa độ điểm đối xứng của A qua d.
= 
= 
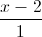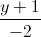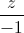và mặt phẳng (P): x + y + z - 3 = 0. Gọi I là giao điểm của ∆ và (P). Tìm tọa độ điểm M thuộc (P) sao cho MI vuông góc với ∆ và MI = 4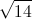
= 
=
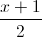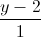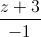1) Viết phương trình tổng quát của mặt phẳng đi qua điểm A và vuông góc với đường thẳng d. 2) Tính khoảng cách từ điểm A đến đường thẳng d. Viết phương trình mặt cầu tâm A, tiếp xúc với d.