(ĐH B -2008) Trong không gian với hệ trục tọa độ Oxyz, cho 3 điểm A(0 ; 1; 2), B(2; -2 ; 1), C( - 2; 0 ;1).a) Viết phương trình mặt phẳng đi qua ba điểm A, B, C.b) Tìm tọa độ điểm M thuộc mặt phẳng : 2x + 2y +z – 3 = 0 sao cho MA = MB = MC.
DANH SÁCH CÂU HỎI
-
[(ĐH B -2008) Trong không gian với hệ trục tọa độ Oxyz, cho 3 điểm A(0 ; 1; 2), B(2; - Luyện Tập 365]
-
[1.Trong không gian với hệ tọa độ Oxyz cho hai điểm A(2; 4; 1), B(-1; 1; 3) và - Luyện Tập 365]
-
[Trong không gian với hệ trục tọa độ Oxyz cho hai điểm A(2; 1 ; 3), B(1; -2; 1) và đ - Luyện Tập 365]
-
[Trong không gian với hệ trục tọa độ Oxyz cho hai điểm A(- 1; 2; 3) và hai mặt phẳng - Luyện Tập 365]
-
[(B – 2010): Trong không gian với hệ trục tọa độ Oxyz cho các điểm A(1; 0; 0), B(0; - Luyện Tập 365]
-
[Cho mặt phẳng (P) : 3x – y + 2z – 3 = 0. Viết phương trình mặt phẳng (Q) cách (P) m - Luyện Tập 365]
-
[Cho hai mặt phẳng (P) : x + y – 2z + 1 = 0 và (Q): 2x – y + 3 = 0. Viết phương trìn - Luyện Tập 365]
-
[Trong không gian với hệ trục tọa độ Oxyz cho hai đường thẳng d1, d2 - Luyện Tập 365]
-
[Trong không gian với hệ trục tọa độ Oxyz cho các điểm A(1; 2; 3), B(0; - 1; 2), C(1 - Luyện Tập 365]
-
[Trong không gian với hệ trục tọa độ Oxyz cho hai điểm A( - 1; 2; - 3), B(2; - 1; - - Luyện Tập 365]
-
[Trong không gian với hệ trục tọa độ Oxyz cho 3 điểm A(1; 1; - 1), B(1; 1; 2), C( - - Luyện Tập 365]
-
[Viết phương trình đường thẳng đi qua M(1; 1; 2) và song song với đường thẳng d : - Luyện Tập 365]
-
[(ĐH D – 2007): Trong không gian với hệ trục tọa độ Oxyz cho 2 điểm A(1; 4; 2), B( - - Luyện Tập 365]
-
[Trong không gian với hệ trục tọa độ Oxyz cho đường thẳng d và mặt phẳng (P) có phươ - Luyện Tập 365]
-
[Trong không gian với hệ trục tọa độ Oxyz cho M(2; 1; 0) và đường thẳng d có phương - Luyện Tập 365]
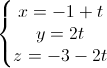. Viết phương trình mặt phẳng (P) qua A, B và song song với d.
.
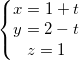; d2 : 
= 
= 
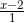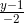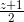. Viết phương trình mặt phẳng (P) song song với d1 và d2 sao cho khoảng cách từ d1 đến (P) gấp hai lần khoảng cách từ d2 đến (P).
.
?
= 
= 
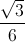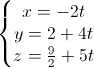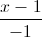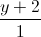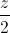. 1)Viết phương trình đường thẳng d đi qua trọng tâm G của tam giác OAB và vuông góc với mặt phẳng (OAB).2)Tìm M ∈∆ sao cho MA2 + MB2 nhỏ nhất.
= 
= 
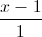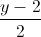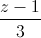; (P): x + y + z + 1 = 0. Viết phương trình hình chiếu vuông góc của d lên (P)?
= 
= 
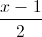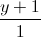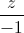. Viết phương trình đường thẳng ∆ đi qua M, cắt và vuông góc với đường thẳng d và tìm tạo độ điểm M’ đối xứng với M qua d.