Trong không gian Oxyz, cho ba điểm A(2;1;-1), B(1;3;1), C(1;2;0). Viết phương trình đường thẳng (d) qua A, vuông góc và cắt đường thẳng BC.
DANH SÁCH CÂU HỎI
-
[Trong không gian Oxyz, cho ba điểm A(2;1;-1), B(1;3;1), C(1;2;0). Viết phương trình đường - Luyện Tập 365]
-
[Cho đường thẳng d: ; (P) x + y + z - 1 = 0 Viết phương trình mặt cầu (S) có tâm thuộc - Luyện Tập 365]
-
[Cho 3 điểm A(1;2;1) ; B(1;0;2) ; C(-1;1;1) 1) Chứng minh 3 điểm không thẳng hàng 2) Tìm - Luyện Tập 365]
-
[Cho tam giác ABC với A(1;1;1); B(-1;0;2). C thuộc trục Ox. Tìm tọa độ điểm C sao cho tam - Luyện Tập 365]
-
[Cho hình hộp ABCDA'B'C'D' với A(1,1,1), B(3,2,1), D(1,2,1), B'(-1,0,2). Tìm tọa độ C', D' - Luyện Tập 365]
-
[Cho hình trụ ABC.A'B'C' có đáy là tam giác đều cạnh a . Hình chiếu vuông gó của A' trên - Luyện Tập 365]
-
[Trong không gian với hệ tọa độ Oxyz , cho mặt phẳng (P) : 6x + 3y - 2z - 1 = 0 và mặt cầu - Luyện Tập 365]
-
[(1 điểm). Trong không gian hệ tọa độ Oxyz , cho mặt phẳng (P) : 2x + y – 2z – 1 = 0 và - Luyện Tập 365]
-
[Trong không gian với hệ toạn độ Oxyz , cho điểm A(1;0;-1) và đường thẳng d : - Luyện Tập 365]
-
[(1,0 điểm): Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, SD = , hình chiếu vuông - Luyện Tập 365]
-
[Trong mặt phẳng với hệ tọa độ Oxy , cho hình bình hành ABCD . Điểm M(-3; 0) là trung điểm - Luyện Tập 365]
-
[Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng (P):2x − y − z +1= 0 và các đường thẳng - Luyện Tập 365]
-
[Trong không gian với hệ tọa độ Oxy cho điểm A(0;0;1), đường thẳng ∆ : = = và - Luyện Tập 365]
-
[Trong không gian với hệ tọa độ Oxyz cho mặt cầu (S) : x2 + y2 + z2= 1 và mặt phẳng - Luyện Tập 365]
-
[Trong không gian với hệ toạ độ Oxyz, cho đường thẳng d : = = và - Luyện Tập 365]
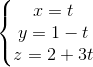; (P) x + y + z - 1 = 0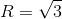
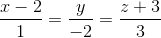. Tìm tọa độ giao điểm của d và (P). Viết phương trình mặt phẳng chứa d và vuông góc với (P).
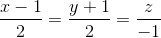. Viết phương trình mặt phẳng qua A và vuông góc với d .
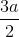, hình chiếu vuông góc của S trên mặt phẳng (ABCD) là trung điểm của cạnh AB. Tính theo a thể tích khối chóp S.ABCD và khoảng cách từ A đến mặt phẳng (SBD).
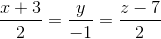; d1: 
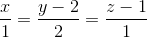; d2: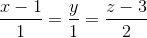 
. Tìm M ∊ d1, N ∊ d2 sao cho đường thẳng MN song song với (P) đồng thời tao với d một góc α sao cho cosα = 
.
= 
= 
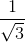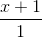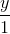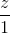và mặt phẳng (P) : x + 2y + z = 1. Tìm trên đường thẳng ∆ hai điểm B và C sao cho tam giác ABC vuông tại A và có trọng tâm G nằm trên mặt phẳng (P)
= 
= 
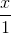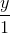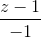và mặt phẳng (P) : 2x +y −2z −3 = 0 . Viết phương trình đường thẳng ∆ vuông góc với mặt phẳng (P), cắt trục hoành và cắt đường thẳng d.