Trong mặt phẳng tọa độ Oxy cho tam giác ABC có đỉnh B(1; 5) và phương trình đường cao AD: x + 2y - 2 = 0 đường phân giác góc C là CC’: x - y - 1 = 0. Tính tọa độ các đỉnh A và C.
DANH SÁCH CÂU HỎI
-
[Trong mặt phẳng tọa độ Oxy cho tam giác ABC có đỉnh B(1; 5) và phương trình đường cao AD: - Luyện Tập 365]
-
[Trong mặt Oxy cho A(0; 2), B(1; 0), C(-1; 0). Viết phương trình đường tròn (C) tiếp xúc - Luyện Tập 365]
-
[Trong mặt phẳng Oxy cho đường tròn (C): x2 + y2 – 6x + 5 = 0. Tìm điểm M thuộc trục tung - Luyện Tập 365]
-
[Trong mặt phẳng Oxy, cho hình vuông ABCD. Gọi M là trung điểm BC, N là điểm trên cạnh CD - Luyện Tập 365]
-
[Trong mặt phẳng với hệ tọa độ Oxy cho đường tròn (C): x2 + y2 + 2x - 6y + 2 = 0 và đường - Luyện Tập 365]
-
[Trong mặt phẳng tọa độ Oxy, cho tam giác ABC vuông tại A, biết rằng B và C đối xứng nhau - Luyện Tập 365]
-
[Trong mặt phẳng Oxy, cho tam giác ABC. Biết phương trình các đường thẳng chứa đường cao - Luyện Tập 365]
-
[Trong mặt phẳng Oxy, cho hình thoi ABCD có đường chéo AC: x + y – 1 = 0. Điểm M(4; 9) nằm - Luyện Tập 365]
-
[Trong mặt phẳng tọa độ Oxy cho hình vuông ABCD có đỉnh A(1; 3), đường chéo BD có phương - Luyện Tập 365]
-
[Trong mặt phẳng với hệ tọa độ Oxy cho đường tròn (C): (x - 3)2 + (y - 1)2 = 9 và đường - Luyện Tập 365]
-
[Trong mặt phẳng với hệ tọa độ Oxy cho tam giác ABC vuông tại A, biết B và C đối xứng nhau - Luyện Tập 365]
-
[Trong mặt phẳng với hệ tọa độ Oxy, cho đường tròn (C): x2 + y2 - 2x + 4y - 3 = 0. Viết phương - Luyện Tập 365]
-
[Trong mặt phẳng với hệ tọa độ Oxy cho tam giác ABC. Trung tuyến kẻ từ A và đường cao kẻ - Luyện Tập 365]
-
[Trong mặt phẳng cho n đường thẳng đôi một cắt nhau sao cho không có ba đường nào đồng quy. - Luyện Tập 365]
-
[Trong mặt phẳng với hệ tọa độ Oxy cho hai điểm A(0; 4), B(5; 0) và đường thẳng (d): 2x − - Luyện Tập 365]
; 
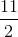) và phương trình đường thẳng AN: 2x – y – 3 = 0. Gọi P là giao điểm của AN và đường chéo BD. Viết phương trình đường thẳng MP và tìm tọa độ P.